Advertisements
Advertisements
Question
In following figure, three circles each of radius 3.5 cm are drawn in such a way that each of them touches the other two. Find the area enclosed between these three circles (shaded region). `["Use" pi=22/7]`

Solution
The given information can be diagrammatically represented as follows:
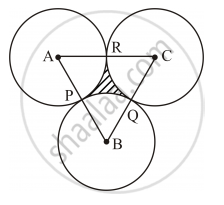
Here, A, B and C are the centres of the circles.
Radius of each circle, r = 3.5 cm
Thus, the measure of each of the sides of ΔABC is 3.5 cm + 3.5 cm = 7 cm.
Since the sides of triangle ABC are of equal lengths, it is an equilateral triangle.
∴ ∠A = ∠B = ∠C = 60°
Area of the shaded region = Area of ΔABC − (sum of areas of sectors APR, BPQ and CQR)
`=sqrt3/4a^2-3xxO//360^@xxpir`
`=1.732/4xx(7"cm")^2-3xx60^@/360^@xx22/7xx3.5"cm"xx3.5"cm"`
`=21.217 "cm"^2-19.25cm^2`
`=1.97"cm"^2`
APPEARS IN
RELATED QUESTIONS
From an external point P, tangents PA and PB are drawn to a circle with center O. If CD is the tangent to the circle at a point E and PA = 14cm, find the perimeter of ΔPCD.

On a semi-circle with AB as diameter, a point C is taken, so that m (∠CAB) = 30°. Find m(∠ACB) and m (∠ABC).
AB and CD are common tangents to two circles of equal radii. Prove that AB = CD.
In the given circle with diameter AB, find the value of x.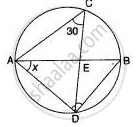
In the figure, O is the centre of the circle, and ∠AOB = 90°, ∠ABC = 30°. Then find ∠CAB.

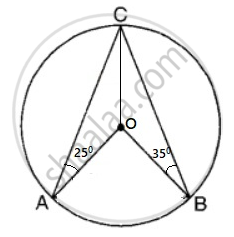
In the adjoining figure ‘O’ is the center of the circle, ∠CAO = 25° and ∠CBO = 35°. What is the value of ∠AOB?
The circumcentre of the triangle ABC is O. Prove that ∠OBC + ∠BAC = 90º.
In the following figure, O is the centre of the circle, BD = OD and CD ⊥ AB. Find ∠CAB.
Say true or false:
Two diameters of a circle will necessarily intersect.
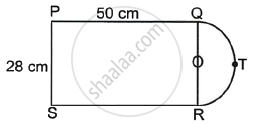
A figure is in the form of rectangle PQRS having a semi-circle on side QR as shown in the figure. Determine the area of the plot.