Advertisements
Advertisements
प्रश्न
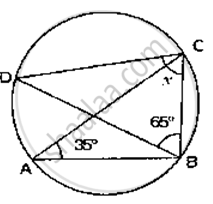
If O is the centre of the circle, find the value of x in the following figure
उत्तर
We have
∠ABD = 40°
∴ ∠ ACD = ∠ABD = 40°
In ΔPCD, By angle sum property
∠PCD + ∠CPO + ∠PDC = 180°
⇒ 40° +110° + x° = 180°
⇒ x° = 180° -150°
⇒x = 30°
APPEARS IN
संबंधित प्रश्न
Prove that a diameter of a circle which bisects a chord of the circle also bisects the angle subtended by the chord at the centre of the circle.
If O is the centre of the circle, find the value of x in the following figure:

If O is the centre of the circle, find the value of x in the following figure
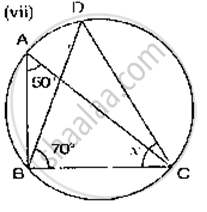
In the given figure, it is given that O is the centre of the circle and ∠AOC = 150°. Find ∠ABC.

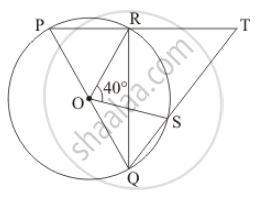
In the given figure, O is the centre of a circle and PQ is a diameter. If ∠ROS = 40°, find ∠RTS.
In the given figure, two congruent circles with centres O and O' intersect at A and B. If ∠AOB = 50°, then find ∠APB.

In the given figure, if O is the circumcentre of ∠ABC, then find the value of ∠OBC + ∠BAC.

If ABC is an arc of a circle and ∠ABC = 135°, then the ratio of arc \[\stackrel\frown{ABC}\] to the circumference is ______.
If arcs AXB and CYD of a circle are congruent, find the ratio of AB and CD.
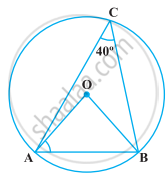
In the following figure, ∠ACB = 40º. Find ∠OAB.