Advertisements
Advertisements
Question
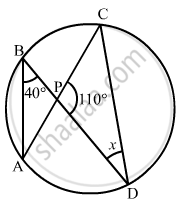
If O is the centre of the circle, find the value of x in the following figures.
Solution

∠ABC = ∠ACD = 40° (Angle in the same segment)
In Δ PCD we have
∠CPD + ∠PCD + ∠PDC = 180°
40 ° + 110 ° + ∠PDC = 180°
∠PDC = 180° -150°
=30°
Hence X = 30 °
APPEARS IN
RELATED QUESTIONS
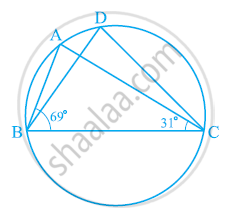
In the given figure, ∠ABC = 69°, ∠ACB = 31°, find ∠BDC.
Prove that the line joining the mid-point of a chord to the centre of the circle passes through the mid-point of the corresponding minor arc.
In the below fig. O is the centre of the circle. Find ∠BAC.
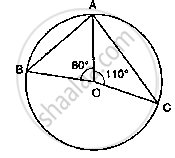
If O is the centre of the circle, find the value of x in the following figures.

O is the circumcentre of the triangle ABC and OD is perpendicular on BC. Prove that ∠BOD = ∠A
Prove that the angle in a segment greater than a semi-circle is less than a right angle.
Prove that the line segment joining the mid-point of the hypotenuse of a right triangle to its opposite vertex is half the hypotenuse.
If the given figure, AOC is a diameter of the circle and arc AXB = \[\frac{1}{2}\] arc BYC. Find ∠BOC.
If ABC is an arc of a circle and ∠ABC = 135°, then the ratio of arc \[\stackrel\frown{ABC}\] to the circumference is ______.
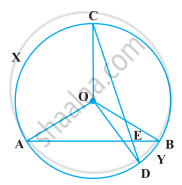
In the following figure, AB and CD are two chords of a circle intersecting each other at point E. Prove that ∠AEC = `1/2` (Angle subtended by arc CXA at centre + angle subtended by arc DYB at the centre).