Advertisements
Advertisements
Question
Prove that a diameter of a circle which bisects a chord of the circle also bisects the angle subtended by the chord at the centre of the circle.
Solution
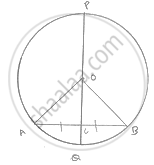
Given: PQ is a diameter of circle which Bisects
Chord AB at C
To prove: PQ bisects ∠AOB
Proof:
In ΔAOC and ΔBOC
OA=OB
OC=OC
AC=BC
Then Δ AOC ≅ BOC
∴∠AOC = ∠BOC
Hence PQ bisects ∠AOB
APPEARS IN
RELATED QUESTIONS
Given an arc of a circle, show how to complete the circle.
If O is the centre of the circle, find the value of x in the following figure

If O is the centre of the circle, find the value of x in the following figures.
If O is the centre of the circle, find the value of x in the following figures.

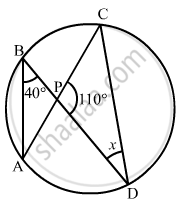
In the given figure, O is the centre of a circle and PQ is a diameter. If ∠ROS = 40°, find ∠RTS.
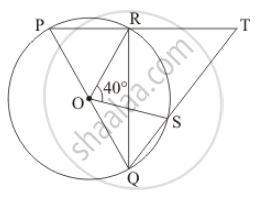
In the given figure, if ∠AOB = 80° and ∠ABC = 30°, then find ∠CAO.

In the given figure, A is the centre of the circle. ABCD is a parallelogram and CDE is a straight line. Find ∠BCD : ∠ABE.

In a circle, the major arc is 3 times the minor arc. The corresponding central angles and the degree measures of two arcs are
If arcs AXB and CYD of a circle are congruent, find the ratio of AB and CD.
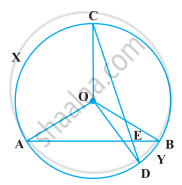
In the following figure, AB and CD are two chords of a circle intersecting each other at point E. Prove that ∠AEC = `1/2` (Angle subtended by arc CXA at centre + angle subtended by arc DYB at the centre).