Advertisements
Advertisements
Question
If O is the centre of the circle, find the value of x in the following figure

Solution
We have
∠AOC = 120°
By degree measure theorem
∠AOC = 2∠APC
⇒ 120° = 2∠APC
⇒∠APC= `(120°)/2=60°`
∴∠APC + ∠ABC = 180°
⇒ 60° + ∠ABC = 180°
⇒ -60° +180° = ∠ABC
⇒ ∠ABC = 120°
∴∠ABC + ∠DBC = 180°
⇒120 + x = 180°
⇒ x = 180° -120° = 60°
APPEARS IN
RELATED QUESTIONS
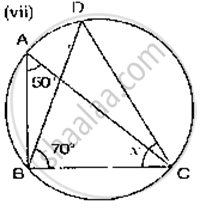
If O is the centre of the circle, find the value of x in the following figure:

If O is the centre of the circle, find the value of x in the following figure
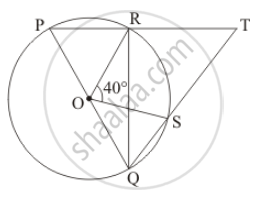
In the given figure, O is the centre of a circle and PQ is a diameter. If ∠ROS = 40°, find ∠RTS.
Prove that the angle in a segment shorter than a semicircle is greater than a right angle.
Prove that the line segment joining the mid-point of the hypotenuse of a right triangle to its opposite vertex is half the hypotenuse.
In the given figure, two congruent circles with centres O and O' intersect at A and B. If ∠AOB = 50°, then find ∠APB.

In the given figure, AB is a diameter of the circle such that ∠A = 35° and ∠Q = 25°, find ∠PBR.

If ABC is an arc of a circle and ∠ABC = 135°, then the ratio of arc \[\stackrel\frown{ABC}\] to the circumference is ______.
A chord of a circle is equal to its radius. Find the angle subtended by this chord at a point in major segment.
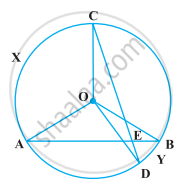
In the following figure, AB and CD are two chords of a circle intersecting each other at point E. Prove that ∠AEC = `1/2` (Angle subtended by arc CXA at centre + angle subtended by arc DYB at the centre).