Advertisements
Advertisements
Question
If O is the centre of the circle, find the value of x in the following figure
Solution
We have
∠ DBO = 40°
∠ DBC = 90°
⇒ ∠ DBO + ∠OBC = 90°
⇒ 40° + ∠OBC = 90°
⇒ ∠ OBC = 90° - 40° = 50°
By degree measure theorem
ÐAOC = 2ÐOBC
⇒ x = 2´ 50° = 100°
APPEARS IN
RELATED QUESTIONS
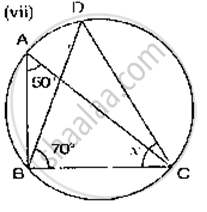
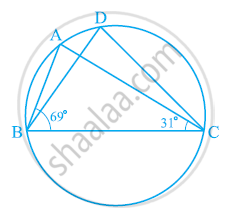
In the given figure, ∠ABC = 69°, ∠ACB = 31°, find ∠BDC.
Prove that the line joining the mid-point of a chord to the centre of the circle passes through the mid-point of the corresponding minor arc.
If O is the centre of the circle, find the value of x in the following figure:

If O is the centre of the circle, find the value of x in the following figures.
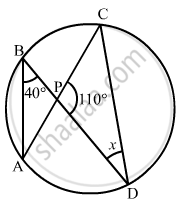
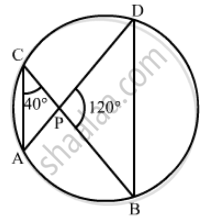
In the given figure, if ∠ACB = 40°, ∠DPB = 120°, find ∠CBD.
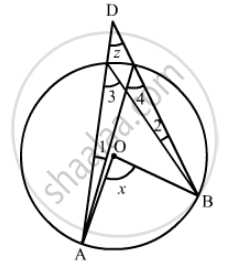
In the given figure, O is the centre of the circle, prove that ∠x = ∠y + ∠z.
In the given figure, if ∠AOB = 80° and ∠ABC = 30°, then find ∠CAO.

In the given figure, P and Q are centres of two circles intersecting at B and C. ACD is a straight line. Then, ∠BQD =
If ABC is an arc of a circle and ∠ABC = 135°, then the ratio of arc \[\stackrel\frown{ABC}\] to the circumference is ______.
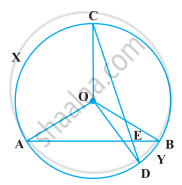
In the following figure, AB and CD are two chords of a circle intersecting each other at point E. Prove that ∠AEC = `1/2` (Angle subtended by arc CXA at centre + angle subtended by arc DYB at the centre).