Question

A solid cone of base radius 10 cm is cut into two part through the mid-point of its height, by a plane parallel to its base. Find the ratio in the volumes of two parts of the cone.

Answer 1

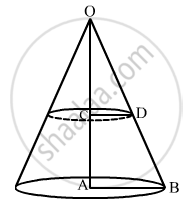
Let the height of the cone be H.
Now, the cone is divided into two parts by the parallel plane
∴ OC = CAH2
Now, In ∆OCD and OAB
∠OCD = OAB          (Corresponding angles)
∠ODC = OBA          (Corresponding angles)
By AA-similarity criterion ∆OCD ∼ ∆OAB

\[\therefore \frac{CD}{AB} = \frac{OC}{OA}\]

\[ \Rightarrow \frac{CD}{10} = \frac{H}{2 \times H}\]

\[ \Rightarrow CD = 5 cm\]

\[\frac{\text { Volume of first part }}{\text { Volume of second part }} = \frac{\frac{1}{3}\pi \left( CD \right)^2 \left( OC \right)}{\frac{1}{3}\pi CA\left[ \left( AB \right)^2 + \left( AB \right)\left( CD \right) + {CD}^2 \right]}\]

\[ = \frac{\left( 5 \right)^2}{\left[ \left( 10 \right)^2 + \left( 10 \right)\left( 5 \right) + 5^2 \right]}\]

\[ = \frac{25}{100 + 50 + 25}\]

\[ = \frac{25}{175}\]

\[ = \frac{1}{7}\]