Advertisements
Advertisements
प्रश्न
A solid cone of base radius 10 cm is cut into two part through the mid-point of its height, by a plane parallel to its base. Find the ratio in the volumes of two parts of the cone.
उत्तर
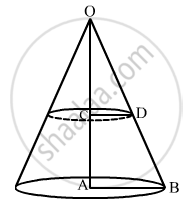
Let the height of the cone be H.
Now, the cone is divided into two parts by the parallel plane
∴ OC = CAH2
Now, In ∆OCD and OAB
∠OCD = OAB (Corresponding angles)
∠ODC = OBA (Corresponding angles)
By AA-similarity criterion ∆OCD ∼ ∆OAB
\[\therefore \frac{CD}{AB} = \frac{OC}{OA}\]
\[ \Rightarrow \frac{CD}{10} = \frac{H}{2 \times H}\]
\[ \Rightarrow CD = 5 cm\]
\[\frac{\text { Volume of first part }}{\text { Volume of second part }} = \frac{\frac{1}{3}\pi \left( CD \right)^2 \left( OC \right)}{\frac{1}{3}\pi CA\left[ \left( AB \right)^2 + \left( AB \right)\left( CD \right) + {CD}^2 \right]}\]
\[ = \frac{\left( 5 \right)^2}{\left[ \left( 10 \right)^2 + \left( 10 \right)\left( 5 \right) + 5^2 \right]}\]
\[ = \frac{25}{100 + 50 + 25}\]
\[ = \frac{25}{175}\]
\[ = \frac{1}{7}\]
APPEARS IN
संबंधित प्रश्न
The radii of the ends of a frustum are 14 cm and 6 cm respectively and its height is 6 cm. Find its curved surface area.
A cone of maximum size is carved out from a cube of edge 14 cm. Find the surface area of the cone and of the remaining solid left out after the cone carved out.
An icecream cone full of icecream having radius 5 cm and height 10 cm as shown in fig. 16.77. Calculate the volume of icecream , provided that its 1/ 6 part is left unfilled with icecream .
If r1 and r2 denote the radii of the circular bases of the frustum of a cone such that r1 > r2, then write the ratio of the height of the cone of which the frustum is a part to the height fo the frustum.
A bucket made up of a metal sheet is in the form of frustum of a cone. Its depth is 24 cm and the diameters of the top and bottom are 30 cm and 10 cm, respectively. Find the cost of completely filling the bucket with milk at the rate of Rs 20 per litre and the cost of metal sheet used if it costs Rs 10 per 100 cm2.
The radii of the circular ends of a solid frustum of a cone are 33 cm and 27 cm and its slant height is 10 cm. Find its total surface area. [Use π = 3.14.]
The diameters of two circular ends of a bucket are 44 cm and 24 cm, and the height of the bucket is 35 cm. The capacity of the bucket is
A shuttle cock used for playing badminton has the shape of a combination of ______.
The number of conical bottles of radius 2 cm and height 3.6 cm, required to empty the liquid from a cylindrical bottle of radius 6 cm and height 10 cm is ______.
If radius of the base of cone is 7 cm and height is 24 cm, then find its slant height.
