Advertisements
Advertisements
Question
The height of a cone is 30 cm. From its topside a small cone is cut by a plane parallel to its base. If volume of smaller cone is `1/27` of the given cone, then at what height it is cut from its base?
Solution
Let the radius and height of the bigger cone be R and H, respectively.
Given: H = 30 cm
Let the radius and height of the smaller cone be r and h, respectively.
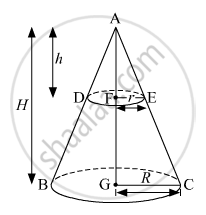
Now, in ∆AFE and ∆AGC,
∠AEF = ∠ACG (Corresponding angles)
∠AFE = ∠AGC (90° each)
∴ ∆AFE~∆AGC (AA similarity)
`=> (AF)/(AG) = (FE)/(GC)`
`=> h/H = r/R` ....(1)
it is given that
Volume of the smaller cone = `1/27 xx "Volume of the bigger cone"`
`=> 1/3 pir^2h = 1/27 xx 1/3 piR^2H`
`=>(r/R)^2 xx h/H = 1/27`
`=> (h/H)^2 xx h/H = 1/27` [Using (1)]
`=> (h/H)^3 = 1/27`
`=> h/H = 1/3`
`:. h = 1/3 xx H = 1/3 xx 30` = 10 cm
Now
FG = AG − AF = 30 cm − 10 cm = 20 cm
Thus, the small cone is cut at the height of 20 cm from the base.
APPEARS IN
RELATED QUESTIONS
Derive the formula for the volume of the frustum of a cone.
If a cone of radius 10 cm is divided into two parts by drawing a plane through the mid-point of its axis, parallel to its base. Compare the volumes of the two parts.
If r1 and r2 denote the radii of the circular bases of the frustum of a cone such that r1 > r2, then write the ratio of the height of the cone of which the frustum is a part to the height fo the frustum.
If the areas of circular bases of a frustum of a cone are 4 cm2 and 9 cm2 respectively and the height of the frustum is 12 cm. What is the volume of the frustum?
The radii of the circular ends of a solid frustum of a cone are 18 cm and 12 cm and its height is 8 cm. Find its total surface area. [Use π = 3.14]
A bucket is in the form of a frustum of a cone. Its depth is 15 cm and the diameters of the top and the bottom are 56 cm and 42 cm, respectively. Find how many litres of water can the bucket hold.
A tent consists of a frustum of a cone, surmounted by a cone. If the diameter of the upper and lower circular ends of the frustum be 14 m and 26 m, respectively, the height of the frustum be 8 m and the slant height of the surmounted conical portion be 12 m, find the area of the canvas required to make the tent. (Assume that the radii of the upper circular end of the frustum and the base of the surmounted conical portion are equal.)
A cylindrical pencil sharpened at one edge is combination of ______.
A cylinder and a cone area of same base radius and of same height. The ratio of the volume of cylinder to that of cone is ______.
An open metallic bucket is in the shape of a frustum of a cone, mounted on a hollow cylindrical base made of the same metallic sheet. The surface area of the metallic sheet used is equal to curved surface area of frustum of a cone + area of circular base + curved surface area of cylinder.
