Advertisements
Advertisements
Question
If a cone of radius 10 cm is divided into two parts by drawing a plane through the mid-point of its axis, parallel to its base. Compare the volumes of the two parts.
Solution
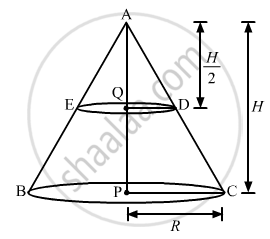
Consider a cone of radius R and height H.
Let a cone of height `H/2` is cutout from this cone whose base is parallel to the original cone. Now is
`Delta AQD and Delta APC, QD || PC`
`Delta AQD ∼ Delta APC`
`(QD)/(PC) = (AQ)/(AP)`
`QD/2 = H/(2/H)`
`QD = R/2`
Volume of cone ABC `=1/3 pi R^2 H`
Volume of cone ADE
`=1/3 pi (R/2)^2 (H/2)`
`=1/8[1/3 piR^2H]`
`=1/8`volume of cone ABC
Now volume of remaining frustum of cons EDCB
= volume of cone ABC − volume of cone AED
\[= \frac{7}{8}(\text { volume of cone ABC})\]
Comparing the volume of cone AED and frustum EDBC we get, the ratio 1 : 7.
APPEARS IN
RELATED QUESTIONS
A solid metallic sphere of radius 10.5 cm is melted and recast into a number of smaller cones, each of radius 3.5 cm and height 3 cm. Find the number of cones so formed.
A solid right circular cone of height 120 cm and radius 60 cm is placed in a right circular cylinder full of water of height 180 cm such that it touches the bottom . Find the volume of water left in the cylinder , if the radius of the cylinder is equal to the radius of te cone
A solid toy s in the form of a hemisphere surrounded by a right circular cone . The height of cone is 4 cm and the diameter of the base is 8 cm . Determine the volume of the toy. If a cube circumscribes the toy , then find the difference of the volumes of cube and the toy .
A rectangular vessel of dimensions 20 cm × 16 cm × 11 cm is full of water. This water is poured into a conical vessel. The top of the conical vessel has its radius 10 cm. If the conical vessel is filled completely, determine its height.
The maximum volume of a cone that can be carved out of a solid hemisphere of radius r is
The radii of the circular ends of a solid frustum of a cone are 18 cm and 12 cm and its height is 8 cm. Find its total surface area. [Use π = 3.14]
A container, open at the top, is in the form of a frustum of a cone of height 24 cm with radii of its lower and upper circular ends as 8 cm and 20 cm, respectively. Find the cost of milk which can completely fill the container at the rate of ₹21 per litre.
A bucket is in the form of a frustum of a cone. Its depth is 15 cm and the diameters of the top and the bottom are 56 cm and 42 cm, respectively. Find how many litres of water can the bucket hold.
A cone is cut through a plane parallel to its base and then the cone that is formedon one side of that plane is removed. The new part that is left over on the other side of the plane is called ______.
An open metallic bucket is in the shape of a frustum of a cone, mounted on a hollow cylindrical base made of the same metallic sheet. The surface area of the metallic sheet used is equal to curved surface area of frustum of a cone + area of circular base + curved surface area of cylinder.
