Advertisements
Advertisements
Question
The maximum volume of a cone that can be carved out of a solid hemisphere of radius r is
Options
\[3 \pi r^2\]
- `1/3pir^3`
\[\frac{\pi r^2}{3}\]
\[3 \pi r^3\]
Solution
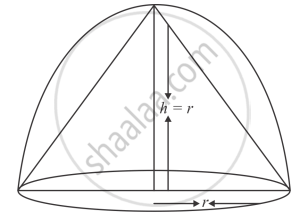
Radius of hemisphere = r
Therefore,
The radius of cone = r
and height h = r
Then,
Volume of cone
`=1/3 pir^2 h `
`=1/3pir^2 xx r`
`=1/3 pir^3 ("unit")^3`
APPEARS IN
RELATED QUESTIONS
Derive the formula for the volume of the frustum of a cone.
A metal container, open from the top, is in the shape of a frustum of a cone of height 21 cm with radii of its lower and upper circular ends as 8 cm and 20 cm respectively. Find the cost of milk which can completely fill the container at the rate of Rs 35 per litre.\[\left[ Use \pi = \frac{22}{7} \right]\]
A washing tub in the shape of a frustum of a cone has a height of 21 cm. The radii of the circular top and bottom are 20 cm and 15 cm respectively. What is the capacity of the tub? ( \[\pi = \frac{22}{7}\]).
If a cone of radius 10 cm is divided into two parts by drawing a plane through the mid-point of its axis, parallel to its base. Compare the volumes of the two parts.
An oil funnel of tin sheet consists of a cylindrical portion 10 cm long attached to a frustum of a cone. If the total height be 22 cm, the diameter of the cylindrical portion 8 cm and the diameter of the top of the funnel 18 cm, find the area of the tin required.(Use π = 22/7).
An icecream cone full of icecream having radius 5 cm and height 10 cm as shown in fig. 16.77. Calculate the volume of icecream , provided that its 1/ 6 part is left unfilled with icecream .
The curved surface area of a right circular cone of height 15 cm and base diameter 16 cm is
The radii of the circular ends of a solid frustum of a cone are 33 cm and 27 cm and its slant height is 10 cm. Find its total surface area. [Use π = 3.14.]
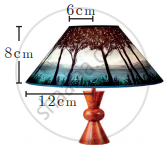
The frustum shaped outer portion of the table lamp has to be painted including the top part. Find the total cost of painting the lamp if the cost of painting 1 sq.cm is ₹ 2.
A bucket is in the form of a frustum of a cone and holds 28.490 litres of water. The radii of the top and bottom are 28 cm and 21 cm, respectively. Find the height of the bucket.
