Advertisements
Advertisements
प्रश्न
The maximum volume of a cone that can be carved out of a solid hemisphere of radius r is
पर्याय
\[3 \pi r^2\]
- `1/3pir^3`
\[\frac{\pi r^2}{3}\]
\[3 \pi r^3\]
उत्तर
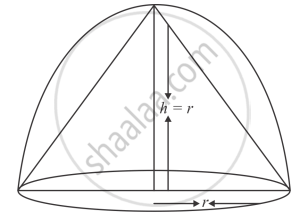
Radius of hemisphere = r
Therefore,
The radius of cone = r
and height h = r
Then,
Volume of cone
`=1/3 pir^2 h `
`=1/3pir^2 xx r`
`=1/3 pir^3 ("unit")^3`
APPEARS IN
संबंधित प्रश्न
A fez, the cap used by the Turks, is shaped like the frustum of a cone (see the figure given below). If its radius on the open side is 10 cm, radius at the upper base is 4 cm and its slant height is 15 cm, find the area of material use for making it. [use π=22/7]

A heap of rice in the form of a cone of diameter 9 m and height 3.5 m. Find the volume of rice. How much canvas cloth is required to cover the heap ?
If a cone of radius 10 cm is divided into two parts by drawing a plane through the mid-point of its axis, parallel to its base. Compare the volumes of the two parts.
An icecream cone full of icecream having radius 5 cm and height 10 cm as shown in fig. 16.77. Calculate the volume of icecream , provided that its 1/ 6 part is left unfilled with icecream .
The radii of the base of a cylinder and a cone are in the ratio 3 : 4 and their heights are in the ratio 2 : 3. What is the ratio of their volumes?
A hemisphere of lead of radius 9 cm is cast into a right circular cone of height 72 cm. Find the radius of the base of the cone.
A container, open at the top, is in the form of a frustum of a cone of height 24 cm with radii of its lower and upper circular ends as 8 cm and 20 cm, respectively. Find the cost of milk which can completely fill the container at the rate of ₹21 per litre.
A bucket made up of a metal sheet is in the form of a frustum of a cone of height 16 cm and radii of its lower and upper ends are 8 cm and 20 cm, respectively. Find the cost of the bucket if the cost of metal sheet used is Rs 15 per 100 cm2.
A tent is made in the form of a frustum of a cone surmounted by another cone. The diameters of the base and the top of the frustum are 20 m and 6 m, respectively, and the height is 24 m. If the height of the tent is 28 m and the radius of the conical part is equal to the radius of the top of the frustum, find the quantity of canvas required.
Choose the correct answer of the following question:
If the height of a bucket in the shape of frustum of a cone is 16 cm and the diameters of its two circular ends are 40 cm and 16 cm, then its slant height is
