Advertisements
Advertisements
प्रश्न
The radii of two cylinders are in the ratio 3 : 5. If their heights are in the ratio 2 : 3, then the ratio of their curved surface areas is
पर्याय
2 : 5
5 : 2
2 : 3
3 : 5
उत्तर
Given that
`r_1 : r_2 = 3: 5` and `h_1 : h_2 = 2 : 3`
Then,
The ratio of C.S.A. of cylinders
`s_1 /s_2 = (2pir_1h_1) / (2pir_2h_2)`
`s_1/s_2 = (r_1/r_2) xx (h_1/h_2)`
`= 3/5 xx 2/3`
`s_1 /s_2 = 2/3`
`s_1 :s_2 = 2:5`
APPEARS IN
संबंधित प्रश्न
A path 2m wide surrounds a circular pond of diameter 40m. how many cubic meters of gravel are required to grave the path to a depth of 20cm ?
Find the volume of the largest right circular cone that can be cut out of a cube where edgeis 9cm?
A circus tent has cylindrical shape surmounted by a conical roof. The radius of the cylindrical base is 20 m. The heights of the cylindrical and conical portions are 4.2 m and 2.1 m respectively. Find the volume of the tent.
A toy is in the form of a hemisphere surmounted by a right circular cone of the same base radius as that of the hemisphere. If the radius of the base of the cone is 21 cm and its volume is `2/3` of the volume of hemisphere, calculate the height of the cone and the surface area of the toy.
`(use pi = 22/7)`
The diameter of a copper sphere is 18 cm. It is melted and drawn into a long wire of uniform cross-section. If the length of the wire is 108 m, find its diameter.
The radius of a solid right circular cylinder decreases by 20% and its height increases by 10%. Find the percentage change in its : volume
The figure shows a running track surrounding a grassed enclosure PQRSTU. The enclosure consists of a rectangle PQST with a semicircular region at each end, PQ = 200 m; PT = 70 meters.
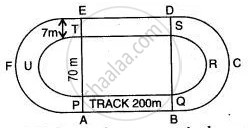
(i) Calculate the area of the grassed enclosure in m2.
(ii) Given that the track is of constant width 7 m, calculate the outer perimeter ABCDEF of the track. (Take π = `22/7`)
Marbles of diameter 1.4 cm are dropped into a cylindrical beaker of diameter 7 cm containing some water. Find the number of marbles that should be dropped into the beaker so that the water level rises by 5.6 cm.
Find the volume of a solid hemisphere whose total surface area is 462 sq.m.
A solid is in the shape of a cone standing on a hemisphere with both their diameters being equal to 1 cm and the height of the cone is equal to its radius. Find the volume of the solid. [Use π = 3.14]
