Advertisements
Advertisements
प्रश्न
Marbles of diameter 1.4 cm are dropped into a cylindrical beaker of diameter 7 cm containing some water. Find the number of marbles that should be dropped into the beaker so that the water level rises by 5.6 cm.
उत्तर
Given, diameter of a marble = 1.4 cm
∴ Radius of marble = `1.4/2` = 0.7 cm
So, volume of one marble
= `4/3 pi(0.7)^3`
= `4/3 pi xx 0.343`
= `1.372/3 pi "cm"^3`
Also, given diameter of beaker = 7 cm
∴ Radius of beaker = `7/2` = 3.5 cm
Height of water level raised = 5.6 cm
∴ Volume of the raised water in beaker
= π(3.5)2 × 5.6
= 68.6π cm3
Now, required number of marbles
= `"Volume of the raised water in beaker"/"Volume of one spherical marble"`
= `(68.6 pi)/(1.372 pi) xx 3`
= 150
APPEARS IN
संबंधित प्रश्न
The difference between outer and inner curved surface areas of a hollow right circular cylinder 14cm long is 88cm2. If the volume of metal used in making cylinder is 176cm3.find the outer and inner diameters of the cylinder____?
A cylindrical tub of radius 5 cm and length 9.8 cm is full of water. A solid in the form of a right circular cone mounted on a hemisphere is immersed in the tub. If the radius of the hemisphere is immersed in the tub. If the radius of the hemi-sphere is 3.5 cm and height of the cone outside the hemisphere is 5 cm, find the volume of the water left in the tub (Take π = 22/7)
If the radii of the circular ends of a conical bucket which is 45 cm high be 28 cm and 7 cm, find the capacity of the bucket. (Use π = 22/7).
The radii of internal and external surfaces of a hollow spherical shell are 3 cm and 5 cm, respectively. It is melted and recast into a solid cylinder of diameter 14 cm. Find the height of the cylinder.
A wooden toy was made by scooping out a hemisphere of same radius from each end of a solid cylinder. If the height of the cylinder is 10 cm and its base is of radius 3.5 cm, then find the volume of wood in the toy.
The sum of the inner and the outer curved surfaces of a hollow metallic cylinder is 1056 cm2 and the volume of material in it is 1056 cm3. Find its internal and external radii. Given that the height of the cylinder is 21 cm.
A piece of paper is in the shape of a semi-circular region of radius 10 cm. It is rolled to form a right circular cone. The slant height is ______.
500 persons are taking a dip into a cuboidal pond which is 80 m long and 50 m broad. What is the rise of water level in the pond, if the average displacement of the water by a person is 0.04m3?
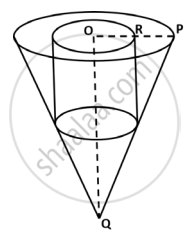
A solid piece of wooden cone is of radius OP = 7 cm and height OQ = 12 cm. A cylinder whose radius and height equal to half of that of the cone is drilled out from this piece of wooden cone. Find the volume of the remaining piece of wood. (Use, `pi = 22/7`)
Read the following passage and answer the questions given below.
|
A solid cuboidal toy is made of wood. It has five cone-shaped cavities to hold toy carrots. The dimensions of the toy cuboid are – 10 cm × 10 cm × 8 cm. Each cone carved out – Radius = 2.1 cm and Height = 6 cm
|
- Find the volume of wood carved out to make five conical cavities.
- Find the volume of the wood in the final product.