Advertisements
Advertisements
प्रश्न
A toy is in the form of a hemisphere surmounted by a right circular cone of the same base radius as that of the hemisphere. If the radius of the base of the cone is 21 cm and its volume is `2/3` of the volume of hemisphere, calculate the height of the cone and the surface area of the toy.
`(use pi = 22/7)`
उत्तर
Let the height of the conical part be h.
Radius of the cone = Radius of the hemisphere = r = 21 cm
The toy can be diagrammatically represented as

Volume of the cone = `1/3pir^2h`
Volume of the hemisphere = `2/3pir^3`
According to given information:
Volume of the cone `=2/3`× Volume of the hemisphere
`therefore 1/3pir^2h=2/3xx2/3pir^3`
⇒`h=(2/3xx2/3pir^3)/(1/3pir^2)`
⇒`h=4/3r`
`therefore h=4/3xx21cm =28 cm`
Thus, surface area of the toy = Curved surface area of cone + Curved surface area of hemisphere
= πrl + 2πr2
`=pirsqrt(h^2+r^2)+2pir^2`
`=pir(sqrt(h^2+r^2)+2r)`
`=22/7xx21cm(sqrt((28cm)^2+(21cm)^2)+2xx21cm)`
`=66(sqrt(784+441)+42)cm^2`
`66(sqrt(1225)+42)cm^2`
= 66(35+42) cm2
= 66 x 77 cm2
= 5082 cm2
APPEARS IN
संबंधित प्रश्न
A path 2m wide surrounds a circular pond of diameter 40m. how many cubic meters of gravel are required to grave the path to a depth of 20cm ?
The diameter of a metallic sphere is equal to 9cm. it is melted and drawn into a long wire of diameter 2mm having uniform cross-section. Find the length of the wire?
A copper sphere of radius 3cm is melted and recast into a right circular cone of height 3cm.find radius of base of cone?
A cylindrical container of radius 6 cm and height 15 cm is filled with ice-cream. The whole ice-cream has to be distributed to 10 children in equal cones with hemispherical tops. If the height of the conical portion is 4 times the radius of its base, then find the radius of the ice-cream cone.
A solid piece of iron in the form a cuboid of dimensions (49 cm × 33 cm × 24 cm) is moulded into a solid sphere. The radius of the sphere is ______.
A cubical ice-cream brick of edge 22 cm is to be distributed among some children by filling ice-cream cones of radius 2 cm and height 7 cm up to the brim. How many children will get the ice-cream cones?
The figure shows a running track surrounding a grassed enclosure PQRSTU. The enclosure consists of a rectangle PQST with a semicircular region at each end, PQ = 200 m; PT = 70 meters.
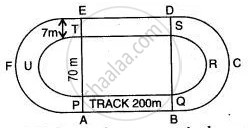
(i) Calculate the area of the grassed enclosure in m2.
(ii) Given that the track is of constant width 7 m, calculate the outer perimeter ABCDEF of the track. (Take π = `22/7`)
A solid piece of iron in the form of a cuboid of dimensions 49 cm × 33 cm × 24 cm, is moulded to form a solid sphere. The radius of the sphere is ______.
How many spherical lead shots each of diameter 4.2 cm can be obtained from a solid rectangular lead piece with dimensions 66 cm, 42 cm and 21 cm.
A building is in the form of a cylinder surmounted by a hemispherical vaulted dome and contains `41 19/21 m^3` of air. If the internal diameter of dome is equal to its total height above the floor, find the height of the building?
