Advertisements
Advertisements
प्रश्न
A cubical ice-cream brick of edge 22 cm is to be distributed among some children by filling ice-cream cones of radius 2 cm and height 7 cm up to the brim. How many children will get the ice-cream cones?
पर्याय
163
263
363
463
उत्तर
363
The edge of the cubical ice - cream brick = a = 22 cm
Volume of the cubical ice - creaam brick = (a)3
`= (22xx22xx22) "cm"^3`
Radius of an ice- cream cone = 2 cm
Height of an ice - cream cone = 7 cm
Volume of each ice - cream cone `= 1/3pi"r"^2"h" `
`= (1/3xx22/7xx2xx2xx7) "cm"^3`
Number of ice - cream cones`= "Volume of the cubical ice cream brick"/"Volume of each ice cream cone"`
`= (22xx22xx22xx3xx7)/(22xx2xx2xx7)`
`=363`
Hence, the number of ice cream cones is 363
APPEARS IN
संबंधित प्रश्न
The diameters of the internal and external surfaces of a hollow spherical shell are 6 cm and 10 cm respectively. If it is melted and recast and recast into a solid cylinder of diameter 14 cm, find the height of the cylinder.
The adjoining figure represents a solid consisting of a cylinder surmounted by a cone at one end and a hemisphere at the other. Find the volume of the solid.
A spherical shell of lead, whose external and internal diameters are 24 cm and 18 cm, is melted and recast into a right circular cylinder 37 cm high. Find the diameter of the base of the cylinder.
A metallic cylinder of radius 8 cm and height 2 cm is melted and converted into a right circular cone of height 6 cm. The radius of the base of this cone is
A hemispherical bowl of internal diameter 30 cm is full of a liquid. This liquid is poured into cylindrical bottles of diameter 5 cm and height 6 cm each. How many bottles are required?
The radius of a solid right circular cylinder increases by 20% and its height decreases by 20%. Find the percentage change in its volume.
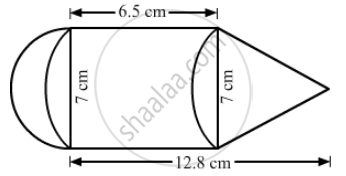
Find the perimeter and area of the shaded portion of the following diagram; give your answer correct to 3 significant figures. (Take π = 22/7).
A piece of paper is in the shape of a semi-circular region of radius 10 cm. It is rolled to form a right circular cone. The slant height is ______.
Three metallic solid cubes whose edges are 3 cm, 4 cm and 5 cm are melted and formed into a single cube. Find the edge of the cube so formed.
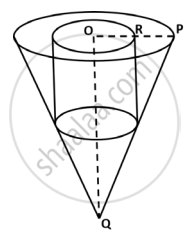
A solid piece of wooden cone is of radius OP = 7 cm and height OQ = 12 cm. A cylinder whose radius and height equal to half of that of the cone is drilled out from this piece of wooden cone. Find the volume of the remaining piece of wood. (Use, `pi = 22/7`)