Advertisements
Advertisements
Question
The frustum shaped outer portion of the table lamp has to be painted including the top part. Find the total cost of painting the lamp if the cost of painting 1 sq.cm is ₹ 2.
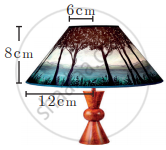
Solution
Slant height of the frustum (l)
= `sqrt("h"^2 + ("R" - "r")^2`
= `sqrt(8^2 + (12 - 6)^2`
= `sqrt(64 + (6)^2`
= `sqrt(64 + 36)`
= `sqrt(100)`
Slant height = 10 m
Total Area to be painted = C.S.A of the Frustum + top area
= πl (R + r) + πr2 sq.units
= π[l (R + r) + r2]
= `22/7[10(12 + 6) + 6^2]`
= `22/7[10 xx 18 + 36] "cm"^2`
= `22/7[180 + 36] "cm"^2`
= `(22 xx 216)/7`
= `4752/7 "cm"^2`
= 678.86 cm2
Cost of painting = ₹ 678.86 × 2 = ₹ 1357.72
APPEARS IN
RELATED QUESTIONS
The slant height of a frustum of a cone is 4 cm and the perimeters (circumference) of its circular ends are 18 cm and 6 cm. find the curved surface area of the frustum.
A heap of rice in the form of a cone of diameter 9 m and height 3.5 m. Find the volume of rice. How much canvas cloth is required to cover the heap ?
A solid cone of base radius 10 cm is cut into two part through the mid-point of its height, by a plane parallel to its base. Find the ratio in the volumes of two parts of the cone.
A bucket, made of metal sheet, is in the form of a cone whose height is 35 cm and radii of circular ends are 30 cm and 12 cm. How many litres of milk it contains if it is full to the brim? If the milk is sold at Rs 40 per litre, find the amount received by the person.
If the slant height of the frustum of a cone is 6 cm and the perimeters of its circular bases are 24 cm and 12 cm respectively. What is the curved surface area of the frustum?
A metallic sphere of radius 10.5 cm is melted and then recast into small cones, each of radius 3.5 cm and height 3 cm. The number of such cones is
The radii of the circular ends of a frustum of height 6 cm are 14 cm and 6 cm, respectively. Find the slant height of the frustum.
A metallic spherical shell of internal and external diameters 4 cm and 8 cm, respectively, is melted and recast in the form of a cone of base diameter 8 cm. The height of the cone is ______.
A drinking glass is in the shape of the frustum of a cone of height 21 cm with 6 cm and 4 cm as the diameters of its two circular ends. Find the capacity of the glass.
An open metallic bucket is in the shape of a frustum of a cone, mounted on a hollow cylindrical base made of the same metallic sheet. The surface area of the metallic sheet used is equal to curved surface area of frustum of a cone + area of circular base + curved surface area of cylinder.
