Advertisements
Advertisements
प्रश्न
The frustum shaped outer portion of the table lamp has to be painted including the top part. Find the total cost of painting the lamp if the cost of painting 1 sq.cm is ₹ 2.
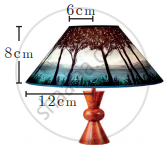
उत्तर
Slant height of the frustum (l)
= `sqrt("h"^2 + ("R" - "r")^2`
= `sqrt(8^2 + (12 - 6)^2`
= `sqrt(64 + (6)^2`
= `sqrt(64 + 36)`
= `sqrt(100)`
Slant height = 10 m
Total Area to be painted = C.S.A of the Frustum + top area
= πl (R + r) + πr2 sq.units
= π[l (R + r) + r2]
= `22/7[10(12 + 6) + 6^2]`
= `22/7[10 xx 18 + 36] "cm"^2`
= `22/7[180 + 36] "cm"^2`
= `(22 xx 216)/7`
= `4752/7 "cm"^2`
= 678.86 cm2
Cost of painting = ₹ 678.86 × 2 = ₹ 1357.72
APPEARS IN
संबंधित प्रश्न
A container open at the top, is in the form of a frustum of a cone of height 24 cm with radii of its lower and upper circular ends, as 8 cm and 20 cm respectively. Find the cost of milk which can completely fill the container. at the rate of 21 per litre. [use π=22/7]
A solid cone of base radius 10 cm is cut into two part through the mid-point of its height, by a plane parallel to its base. Find the ratio in the volumes of two parts of the cone.
A rectangular vessel of dimensions 20 cm × 16 cm × 11 cm is full of water. This water is poured into a conical vessel. The top of the conical vessel has its radius 10 cm. If the conical vessel is filled completely, determine its height.
A frustum of a cone is 9 cm thick and the diameters of its circular ends are 28 cm and 4 cm. Find the volume and lateral surface area of the frustum.
(Take π = 22/7).
A right circular cone and a right circular cylinder have equal base and equal height. If the radius of the base and height are in the ratio 5 : 12, write the ratio of the total surface area of the cylinder to that of the cone.
The height and radius of the cone of which the frustum is a part are h1 and r1 respectively. If h2 and r2 are the heights and radius of the smaller base of the frustum respectively and h2 : h1 = 1 : 2, then r2 : r1 is equal to
A solid metal cone with base radius of 12 cm and height 24 cm is melted to form solid spherical balls of diameter 6 cm each. Find the number of balls thus formed.
A bucket is in the form of a frustum of a cone. Its depth is 15 cm and the diameters of the top and the bottom are 56 cm and 42 cm, respectively. Find how many litres of water can the bucket hold.
A container in the shape of a frustum of a cone having diameters of its two circular faces as 35 cm and 30 cm and vertical height 14 cm,
is completely filled with oil. If each cm3 of oil has mass 1.2 g, then find the cost of oil in the container if it costs ₹40 per kg.
A milk container of height 16 cm is made of metal sheet in the form of frustum of a cone with radii of its lower and upper ends as 8 cm and 20 cm respectively. Find the cost of milk at the rate of ₹ 22 per litre which the container can hold.
