Advertisements
Advertisements
Question
A tent is of the shape of a right circular cylinder upto a height of 3 metres and then becomes a right circular cone with a maximum height of 13.5 metres above the ground. Calculate the cost of painting the inner side of the tent at the rate of Rs 2 per square metre, if the radius of the base is 14 metres.
Solution
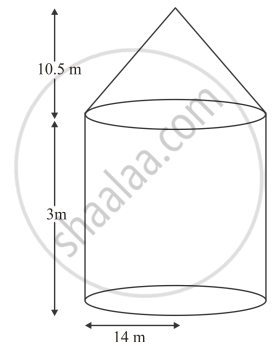
Let r m be the radius of cylindrical base of cylinder of height by m
r = 14 m and h1 = 3m
Curved surface area of cylinder
`=2pirh_1m^2`
`=25 22/7 xx 14 xx 3m^2`
`=264 m^2`
The radius of cylindrical box of cylinder is also equal to the radius of right circular cons.
Let h2 be the height of cone and l be the slant height of cone
`r = 14m and h_2 = (13.5 - 3)`
`=10.5 m`
`l^2 = r^2 + h_2^2`
`l^2 = (14)^2 + (10.5)^2`
`l^2 =(14)^2 + (10.5)^2`
`l = sqrt(196 + 110.25)`
`sqrt(306.25 ) = 17.5 m`
Curved surface area of the cone
`pirl`
`= 22/7 xx 14 xx 17.5`
Curved surface of area of cone
`= pirl`
`= 22/7 xx 14 17.5`
`=770 m^2`
Therefore,
Total area of tent which is to be painted
= curved surface area of cylinder + curved surface area of cone
`=(264+770)m^2`
`=1034 m^2`
Now cost of painting 1 m2 of inner side of tent = Rs. 2
Cost of painting 1034 m2 inner side of tent
`= 2 xx 1034`
`="Rs. 2068"`
APPEARS IN
RELATED QUESTIONS
Metallic spheres of radii 6 cm, 8 cm, and 10 cm, respectively, are melted to form a single solid sphere. Find the radius of the resulting sphere.
A cylindrical bucket, 32 cm high and with radius of base 18 cm, is filled with sand. This bucket is emptied on the ground and a conical heap of sand is formed. If the height of the conical heap is 24 cm. Find the radius and slant height of the heap.
A farmer connects a pipe of internal diameter 20 cm form a canal into a cylindrical tank in his field, which is 10 m in diameter and 2 m deep. If water flows through the pipe at the rate of 3 km/h, in how much time will the tank be filled?
A right circular cylinder of radius r and height h (h = 2r) just encloses a sphere of diameter
The radii of the ends of a bucket 16 cm height are 20 cm and 8 cm. The curved surface area of the bucket is
Metallic spheres of radii 6 cm, 8 cm and 10 cm, respectively are melted to form a single solid sphere. Find the radius of the resulting sphere.
The internal and external diameters of a hollow hemispherical shell are 6 cm and 10 cm, respectively. It is melted and recast into a solid cone of base diameter 14 cm. Find the height of the cone so formed.
During conversion of a solid from one shape to another, the volume of the new shape will ______.
A cylindrical bucket, 32 cm high and 18 cm of radius of the base, is filled with sand. This bucket is emptied on the ground and a conical heap of sand is formed. If the height of the conical heap is 24 cm, find the radius and slant height of the heap.
A solid cylinder of radius r and height h is placed over other cylinder of same height and radius. The total surface area of the shape so formed is ______.
