Question

A tent is of the shape of a right circular cylinder upto a height of 3 metres and then becomes a right circular cone with a maximum height of 13.5 metres above the ground. Calculate the cost of painting the inner side of the tent at the rate of Rs 2 per square metre, if the radius of the base is 14 metres.

Answer 1

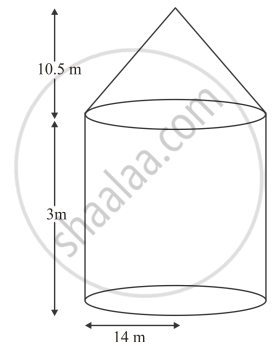
Let r m be the radius of cylindrical base of cylinder of height by m

r = 14 m and h₁ = 3m

Curved surface area of cylinder

`=2pirh_1m^2`

`=25 22/7 xx 14 xx 3m^2`

`=264 m^2`

The radius of cylindrical box of cylinder is also equal to the radius of right circular cons.

Let h₂ be the height of cone and l be the slant height of cone

`r = 14m and h_2 = (13.5 - 3)`

`=10.5 m`

`l^2 = r^2 + h_2^2`

`l^2 = (14)^2 + (10.5)^2`

`l^2 =(14)^2 + (10.5)^2`

`l = sqrt(196 + 110.25)`

`sqrt(306.25 ) = 17.5 m`

Curved surface area of the cone

`pirl`

`= 22/7 xx 14 xx 17.5`

Curved surface of area of cone

`= pirl`

`= 22/7 xx 14 17.5`

`=770 m^2`

Therefore,

Total area of tent which is to be painted

= curved surface area of cylinder + curved surface area of cone

`=(264+770)m^2`

`=1034 m^2`

Now cost of painting 1 m² of inner side of tent = Rs. 2

Cost of painting 1034 m² inner side of tent

`= 2 xx 1034`

`="Rs. 2068"`