Advertisements
Advertisements
प्रश्न
A running track has 2 semicircular ends of radius 63 m and two straight lengths. The perimeter of the track is 1000 m. Find each straight length.
उत्तर
Radius of semi-circular track = 63 m
Perimeter of 2 semi-circles = Perimeter of 1 circle
Perimeter of a circular track = 2πr
Perimeter of circular track = `2 xx 22/7 xx 63`
= 2 × 22 × 9
= 44 × 9
= 396 m
∵ The perimeter of the total track is 1000 m.
∴ Length of two straight lengths track = 1000 – 396 = 604 m
Length of 1 straight length track = `604/2` = 302 m
APPEARS IN
संबंधित प्रश्न
A conical hole is drilled in a circular cylinder of height 12 cm and base radius 5 cm. The height and the base radius of the cone are also the same. Find the whole surface and volume of the remaining cylinder.
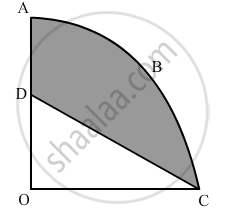
In Figure 3, OABC is a quadrant of a circle of radius 7 cm. If OD = 4 cm, find the area of the shaded region ?\[[Use\pi = \frac{22}{7}]\]
Water flows at the rate of 10 m / minute through a cylindrical pipe 5 mm in diameter . How long would it take to fill a conical vessel whose diameter at the base is 40 cm and depth 24 cm.
Water flows at the rate of 10 metre per minute from a cylindrical pipe 5 mm in diameter. How long will it take to fill up a conical vessel whose diameter at the base is 40 cm and depth 24 cm?
A 5-m-wide cloth is used to make a conical tent of base diameter 14 m and height 24 m. Find the cost of cloth used, at the rate of ₹25 per metre.
If the radii of the circular ends of a bucket 28 cm high, are 28 cm and 7 cm, then find its capacity and total surface area.
The length of the longest pole that can be kept in a room (12 m × 9 m ×8 m) is
Two cubes, each of volume 64 cm3, are joined end to end. Find the total surface area of the resulting cuboid.
How many solid cylinders of radius 6 cm and height 12 cm can be made by melting a solid sphere of radius 18 cm?
Activity: Radius of the sphere, r = 18 cm
For cylinder, radius R = 6 cm, height H = 12 cm
∴ Number of cylinders can be made =`"Volume of the sphere"/square`
`= (4/3 pir^3)/square`
`= (4/3 xx 18 xx 18 xx 18)/square`
= `square`
A cube whose edge is 20 cm long, has circles on each of its faces painted black. What is the total area of the unpainted surface of the cube if the circles are of the largest possible areas?
