Advertisements
Advertisements
Question
If a cone is cut into two parts by a horizontal plane passing through the mid-point of its axis, the ratio of the volumes of the upper part and the cone is
Options
1 : 2
1: 4
1 : 6
1 : 8
Solution
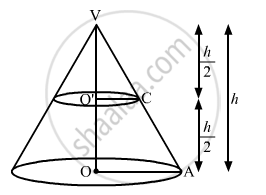
Since,
`Delta VOA ∼ Delta VO'C`
Therefore,
In `Delta VOA ` and `Delta VO'C`
`(h/2)/h = (O'C)/(OA)`
`1/2 =(O'C)/(OA)`
`(O'C)/(OA) = 1/2`
The ratio of the volume of upper part and the cone,
`V_1/V_2 = (1/3pi(O'C) xx h/2)/ (1/3pi(OA)^2 xx h)`
`V_1/V_2 = ((O'C)/(OA))^2 xx 1/2 ........... (2)`
From eq. (1) and (2),
We get,
`V_1/V_2 = (1/2)^2 xx 1/2`
`V_1/V_2 = 1/4 xx 1/2`
`V_1 : V_2 = 1 : 8`
APPEARS IN
RELATED QUESTIONS
A cone of height 20 cm and radius of base 5 cm is made up of modeling clay. A child reshapes it in the form of a sphere. Find the diameter of the sphere.
A heap of rice in the form of a cone of diameter 9 m and height 3.5 m. Find the volume of rice. How much canvas cloth is required to cover the heap ?
The surface area of a sphere is the same as the curved surface area of a cone having the radius of the base as 120 cm and height 160 cm. Find the radius of the sphere.
The radii of the base of a cylinder and a cone are in the ratio 3 : 4 and their heights are in the ratio 2 : 3. What is the ratio of their volumes?
A cone, a hemisphere and a cylinder stand on equal bases and have the same height. What is the ratio of their volumes?
If the areas of circular bases of a frustum of a cone are 4 cm2 and 9 cm2 respectively and the height of the frustum is 12 cm. What is the volume of the frustum?
A container, open at the top, is in the form of a frustum of a cone of height 24 cm with radii of its lower and upper circular ends as 8 cm and 20 cm, respectively. Find the cost of milk which can completely fill the container at the rate of ₹21 per litre.
A tent is made in the form of a frustum of a cone surmounted by another cone. The diameters of the base and the top of the frustum are 20 m and 6 m, respectively, and the height is 24 m. If the height of the tent is 28 m and the radius of the conical part is equal to the radius of the top of the frustum, find the quantity of canvas required.
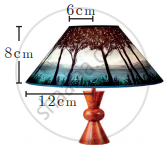
The frustum shaped outer portion of the table lamp has to be painted including the top part. Find the total cost of painting the lamp if the cost of painting 1 sq.cm is ₹ 2.
A metallic spherical shell of internal and external diameters 4 cm and 8 cm, respectively is melted and recast into the form a cone of base diameter 8 cm. The height of the cone is ______.
