Advertisements
Advertisements
Question
The radii of ends of a frustum are 14 cm and 6 cm respectively and its height is 6 cm. Find its total surface area.
Solution
Here, r1 = 14 cm, r2 = 6 cm and h = 6 cm.
Slant height of the frustum,
l = \[\sqrt{h^2 + \left( r_2 - r_1 \right)^2}\]
= \[\sqrt{6^2 + \left( 14 - 6 \right)^2}\]
= \[\sqrt{6^2 + 8^2}\]
= \[\sqrt{36 + 64}\]
= \[\sqrt{100}\]
= 10 cm
Total surface area of frustrum
\[=\pi l(r_{1}+r_{2})+\pi r_{1}{}^{2}+\pi r_{2}{}^{2}\]
\[ = 3 . 14 \times \left( 14 + 6 \right) \times 10 + 3 . 14 \times {14}^2 + 3 . 14 \times 6^2 \]
\[ = 3 . 14 \times 20 \times 10 + 3 . 14 \times 196 + 3 . 14 \times 36\]
\[ = 628 + 615 . 44 + 113 . 04\]
\[ = 1356 . 48 { cm}^2\]
∴ The total surface area of the frustum is 1356.48 cm2.
APPEARS IN
RELATED QUESTIONS
A metallic bucket, open at the top, of height 24 cm is in the form of the frustum of a cone, the radii of whose lower and upper circular ends are 7 cm and 14 cm respectively. Find :
(i) the volume of water which can completely fill the bucket.
(ii) the area of the metal sheet used to make the bucket.
[Use π =\[\frac{22}{7}\]
The radii of ends of a frustum are 14 cm and 6 cm respectively and its height is 6 cm. Find its volume \[\pi\] = 3.14)
A hemisphere of lead of radius 7 cm is cast into a right circular cone of height 49 cm. Find the radius of the base.
The surface area of a sphere is the same as the curved surface area of a cone having the radius of the base as 120 cm and height 160 cm. Find the radius of the sphere.
An icecream cone full of icecream having radius 5 cm and height 10 cm as shown in fig. 16.77. Calculate the volume of icecream , provided that its 1/ 6 part is left unfilled with icecream .
A solid consists of a circular cylinder with an exact fitting right circular cone placed at the top. The height of the cone is h. If the total volume of the solid is 3 times the volume of the cone, then the height of the circular is
A hollow sphere of internal and external diameters 4 cm and 8 cm respectively is melted into a cone of base diameter 8 cm. The height of the cone is
A cone of height 20 cm and radius of base 5 cm is made up of modelling clay. A child reshapes it in the form of a sphere. Find the diameter of the sphere.
A container, open at the top and made up of metal sheet, is in the form of a frustum of a cone of height 16 cm with diameters of its lower and upper ends as 16 cm and 40 cm, respectively. Find the cost of metal sheet used to make the container, if it costs ₹10 per 100 cm2
A bucket made up of a metal sheet is in the form of a frustum of a cone of height 16 cm and radii of its lower and upper ends are 8 cm and 20 cm, respectively. Find the cost of the bucket if the cost of metal sheet used is Rs 15 per 100 cm2.
A tent consists of a frustum of a cone, surmounted by a cone. If the diameter of the upper and lower circular ends of the frustum be 14 m and 26 m, respectively, the height of the frustum be 8 m and the slant height of the surmounted conical portion be 12 m, find the area of the canvas required to make the tent. (Assume that the radii of the upper circular end of the frustum and the base of the surmounted conical portion are equal.)
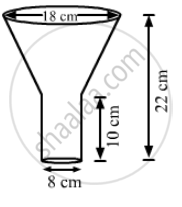
An oil funnel made of tin sheet consists of a 10 cm long cylindrical portion attached to a frustum of a cone. If the total height is 22 cm, diameter of the cylindrical portion is 8 cm and the diameter of the top of the funnel is 18 cm, then find the area of the tin sheet required to make the funnel.
A metallic spherical shell of internal and external diameters 4 cm and 8 cm, respectively, is melted and recast in the form of a cone of base diameter 8 cm. The height of the cone is ______.
A cylinder and a cone area of same base radius and of same height. The ratio of the volume of cylinder to that of cone is ______.
A cone is cut through a plane parallel to its base and then the cone that is formedon one side of that plane is removed. The new part that is left over on the other side of the plane is called ______.
A solid formed on revolving a right-angled triangle about its height is ______.
A shuttle cock used for playing badminton has the shape of the combination of ______.
Find the total surface area of frustum, if its radii are 15 cm and 7 cm. Also, the slant height of the frustum is 14 cm.
Radii of the frustum = `square` cm and `square` cm
Slant height of the frustum = `square` cm
Total surface area = `π[(r_1^2 + r_2^2 + (r_1 + r_2)l]`
= `22/7 [square + square + (square + square) square]`
= `22/7 (square)`
= `square` cm2
Hence, the total surface area of the frustum is `square`.
Find the curved surface area of a right circular cone whose height is 15 cm and base radius is 8 cm. tan β = `3/4`.
