Advertisements
Advertisements
Question
The radii of the ends of a frustum are 14 cm and 6 cm respectively and its height is 6 cm. Find its curved surface area.
Solution
Given: Radii (r1) = 14 cm, r2 = 6 cm, height (h) = 6 cm
Slant height of the frustum (l)
= `sqrt(h^2 + (r_1 - r_2)^2)`
= `sqrt(6^2 + (14 - 6)^2)`
= `sqrt(6^2 + 8^2)`
= `sqrt(36 + 64)`
= `sqrt(100)`
= 10 cm
Curved surface area of the frustum
= πl (r1 + r2)
= 3.14 × 10 (14 + 6)
= 3.14 × 10 × 20
= 628 cm2
∴ The curved surface area of the frustum is 628 cm2.
APPEARS IN
RELATED QUESTIONS
A container, opened from the top and made up of a metal sheet, is in the form of a frustum of a cone of height 16 cm with radii of its lower and upper ends as 8 cm and 20 cm respectively. Find the cost of the milk which can completely fill the container, at the rate of Rs.20 per litre. Also find the cost of metal sheet used to make the container, if it costs Rs.8 per 100 cm2. [Take π = 3.14]
Milk in a container, which is in the form of a frustum of a cone of height 30 cm and the radii of whose lower and upper circular ends are 20 cm and 40 cm respectively, is to be distributed in a camp for flood victims. If this milk is available at the rate of Rs 35 per litre and 880 litres of milk is needed daily for a camp, find how many such containers of milk are needed for a camp and what cost will it put on the donor agency for this. What value is indicated through this by the donor agency ?
A heap of rice in the form of a cone of diameter 9 m and height 3.5 m. Find the volume of rice. How much canvas cloth is required to cover the heap ?
A rectangular vessel of dimensions 20 cm × 16 cm × 11 cm is full of water. This water is poured into a conical vessel. The top of the conical vessel has its radius 10 cm. If the conical vessel is filled completely, determine its height.
A cone of maximum size is carved out from a cube of edge 14 cm. Find the surface area of the cone and of the remaining solid left out after the cone carved out.
An icecream cone full of icecream having radius 5 cm and height 10 cm as shown in fig. 16.77. Calculate the volume of icecream , provided that its 1/ 6 part is left unfilled with icecream .
If the areas of circular bases of a frustum of a cone are 4 cm2 and 9 cm2 respectively and the height of the frustum is 12 cm. What is the volume of the frustum?
A hollow sphere of internal and external diameters 4 cm and 8 cm respectively is melted into a cone of base diameter 8 cm. The height of the cone is
A container, open at the top and made up of metal sheet, is in the form of a frustum of a cone of height 16 cm with diameters of its lower and upper ends as 16 cm and 40 cm, respectively. Find the cost of metal sheet used to make the container, if it costs ₹10 per 100 cm2
A tent is made in the form of a frustum of a cone surmounted by another cone. The diameters of the base and the top of the frustum are 20 m and 6 m, respectively, and the height is 24 m. If the height of the tent is 28 m and the radius of the conical part is equal to the radius of the top of the frustum, find the quantity of canvas required.
A tent consists of a frustum of a cone, surmounted by a cone. If the diameter of the upper and lower circular ends of the frustum be 14 m and 26 m, respectively, the height of the frustum be 8 m and the slant height of the surmounted conical portion be 12 m, find the area of the canvas required to make the tent. (Assume that the radii of the upper circular end of the frustum and the base of the surmounted conical portion are equal.)
The height of a right circular cone is 20 cm. A small cone is cut off at the top by a plane parallel to the base. If its volume be `1/8` of the volume of the given cone, then at what height above the base is the section made?
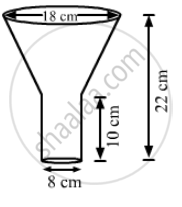
An oil funnel made of tin sheet consists of a 10 cm long cylindrical portion attached to a frustum of a cone. If the total height is 22 cm, diameter of the cylindrical portion is 8 cm and the diameter of the top of the funnel is 18 cm, then find the area of the tin sheet required to make the funnel.
A bucket of height 24 cm is in the form of frustum of a cone whose circular ends are of diameter 28 cm and 42 cm. Find the cost of milk at the rate of ₹30 per litre, which the bucket can hold.
A bucket is in the form of a frustum of a cone with a capacity of 12308.8 cm3 of water. The radii of the top and bottom circular ends are
20 cm and 12 cm, respectively. Find the height of the bucket. [Use π = 3.14]
A solid metallic sphere of diameter 28 cm is melted and recast into a number of smaller cones, each of diameter `"4"2/3` cm and height 3 cm. Find the number of cones so formed.
An open metal bucket is in the shape of a frustum of a cone, mounted on a hollow cylindrical base made of the same metallic sheet. The diameters of the two circular ends of the bucket are 45 cm and 25 cm, the total vertical height of the bucket is 40 cm and that of the cylindrical base is 6 cm. Find the area of the metallic sheet used to make the bucket. Also, find the volume of water the bucket can hold, in litres.
A cylinder and a cone area of same base radius and of same height. The ratio of the volume of cylinder to that of cone is ______.
The number of conical bottles of radius 2 cm and height 3.6 cm, required to empty the liquid from a cylindrical bottle of radius 6 cm and height 10 cm is ______.
