Advertisements
Advertisements
Question
Milk in a container, which is in the form of a frustum of a cone of height 30 cm and the radii of whose lower and upper circular ends are 20 cm and 40 cm respectively, is to be distributed in a camp for flood victims. If this milk is available at the rate of Rs 35 per litre and 880 litres of milk is needed daily for a camp, find how many such containers of milk are needed for a camp and what cost will it put on the donor agency for this. What value is indicated through this by the donor agency ?
Solution
Height of container, h = 30 cm
Lower radius,\[r_1 = 20 cm\]
Upper radius, \[r_2 = 40 cm\]
Volume of container =\[\frac{1}{3}\pi\left( {r_1}^2 + {r_2}^2 + r_1 r_2 \right)h\]
\[= \frac{1}{3} \times \frac{22}{7}\left( {20}^2 + {40}^2 + 20 \times 40 \right)30\]
\[ = \frac{1}{3} \times \frac{22}{7}\left( 400 + 1600 + 800 \right)30\]
\[ = \frac{1}{3} \times \frac{22}{7} \times 2800 \times 30\]
\[ = 88000 {cm}^3 = 88 L\]
Amount of milk needed daily for the camp = 880 L
\[= \frac{1}{3} \times \frac{22}{7}\left( {20}^2 + {40}^2 + 20 \times 40 \right)30\]
\[ = \frac{1}{3} \times \frac{22}{7}\left( 400 + 1600 + 800 \right)30\]
\[ = \frac{1}{3} \times \frac{22}{7} \times 2800 \times 30\]
\[ = 88000 {cm}^3 = 88 L\]
∴ Number of containers required = \[\frac{880 L}{88 L} = 10\]
Also, milk is available at the rate of Rs 35 per litre.
a) Charity
b) Sympathy
c) Humanity
APPEARS IN
RELATED QUESTIONS
A metallic right circular cone 20 cm high and whose vertical angle is 60° is cut into two parts at the middle of its height by a plane parallel to its base. If the frustum so obtained is drawn into a wire of diameter 1/16 cm, find the length of the wire [use π=22/7]
Derive the formula for the curved surface area and total surface area of the frustum of cone.
The radii of ends of a frustum are 14 cm and 6 cm respectively and its height is 6 cm. Find its volume \[\pi\] = 3.14)
A solid right circular cone of height 120 cm and radius 60 cm is placed in a right circular cylinder full of water of height 180 cm such that it touches the bottom . Find the volume of water left in the cylinder , if the radius of the cylinder is equal to the radius of te cone
The surface area of a sphere is the same as the curved surface area of a cone having the radius of the base as 120 cm and height 160 cm. Find the radius of the sphere.
The radii of the ends of a frustum of a right circular cone are 5 metres and 8 metres and its lateral height is 5 metres. Find the lateral surface and volume of the frustum.
A hemisphere of lead of radius 9 cm is cast into a right circular cone of height 72 cm. Find the radius of the base of the cone.
The height of a right circular cone is 20 cm. A small cone is cut off at the top by a plane parallel to the base. If its volume be `1/8` of the volume of the given cone, then at what height above the base is the section made?
An oil funnel made of tin sheet consists of a 10 cm long cylindrical portion attached to a frustum of a cone. If the total height is 22 cm, diameter of the cylindrical portion is 8 cm and the diameter of the top of the funnel is 18 cm, then find the area of the tin sheet required to make the funnel.
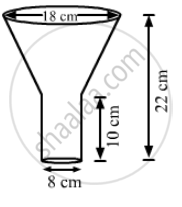
A cone is cut by a plane parallel to its base and the upper part is removed. The part that is left is called

