Advertisements
Advertisements
प्रश्न
The height of a right circular cone is 20 cm. A small cone is cut off at the top by a plane parallel to the base. If its volume be `1/8` of the volume of the given cone, then at what height above the base is the section made?
उत्तर
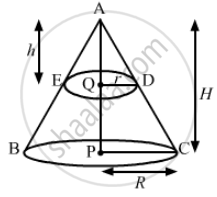
We have,
Height of the given cone, H = 20 cm
Let the radius of the given cone be h and
the height of the smaller cone be r.
Now, in ΔAQD and ΔAPC,
∠QAD = ∠PAC (Common angle)
∠AQD = ∠APC = 90°
So, by AA criteria
∠AQD ˜∠APC
`rArr ("AQ")/"AP"=("QD")/("PC")`
`rArr "h"/"H" = "r"/"R" .......(i)`
Volume of smaller cone `= 1/8xx "Volume of the given cone"`
`rArr "Volume of smaller cone"/"Volume of the given one" = 1/8`
`rArr ((1/3pi"r"^2"h"))/((1/3pi"R"^2"H"))=1/8`
`rArr ("r"/"R")^2xx("h"/"H") = 1/8`
`rArr ("h"/"H")^2xx("h"/"H")=1/8` [Using (i)]
`rArr ("h"/"H")^3 = 1/8`
`rArr "h"/"H"=root(3)(1/8)`
`rArr "h"/"20" = 1/2`
`rArr "h" = 20/2`
`rArr "h" = 10 "cm"`
∴ PQ = H - h = 20 - 10 cm
So, the section is made at the height of 10 cm above the base.
APPEARS IN
संबंधित प्रश्न
A container, opened from the top and made up of a metal sheet, is in the form of a frustum of a cone of height 16 cm with radii of its lower and upper ends as 8 cm and 20 cm respectively. Find the cost of the milk which can completely fill the container, at the rate of Rs.20 per litre. Also find the cost of metal sheet used to make the container, if it costs Rs.8 per 100 cm2. [Take π = 3.14]
The radii of ends of a frustum are 14 cm and 6 cm respectively and its height is 6 cm. Find its total surface area.
The radii of the ends of a frustum of a right circular cone are 5 metres and 8 metres and its lateral height is 5 metres. Find the lateral surface and volume of the frustum.
A bucket is in the form of a frustum of a cone and holds 15.25 litres of water. The diameters of the top and bottom are 25 cm and 20 cm respectively. Find its height and area of tin used in its construction.
A hollow sphere of internal and external diameters 4 cm and 8 cm respectively is melted into a cone of base diameter 8 cm. The height of the cone is
A tent consists of a frustum of a cone, surmounted by a cone. If the diameter of the upper and lower circular ends of the frustum be 14 m and 26 m, respectively, the height of the frustum be 8 m and the slant height of the surmounted conical portion be 12 m, find the area of the canvas required to make the tent. (Assume that the radii of the upper circular end of the frustum and the base of the surmounted conical portion are equal.)
The perimeters of the two circular ends of a frustum of a cone are 48 cm and 36 cm. If the height of the frustum is 11 cm, then find its volume and curved surface area.
A right cylindrical vessel is full of water. How many right cones having the same radius and height as those of the right cylinder will be needed to store that water?
A solid formed on revolving a right-angled triangle about its height is ______.
