Question

A solid metallic right circular cone 20 cm high and whose vertical angle is 60°, is cut into two parts at the middle of its height by a plane parallel to its base. If the frustum so obtained be drawn into a wire of diameter `1/12` cm, then find the length of the wire.

Answer 1

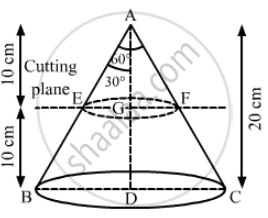
We have,

Height of the metallic cone, H = 20 cm,

Height of the frustum, `"h" = 20/2 = 10  "cm"` and

Radius of the wire `= 1/24  "cm"`

Let the length of the wire be l, EG = r and BD = R

In ΔAEG,

`"tan"30° = "EG"/"AG"`

`rArr 1/sqrt(3) = r/("H"-"h")`

`rArr 1/sqrt(3)="r"/(20-10)`

`rArr r = 10/sqrt(3) "cm"`

Also, in Δ ABD,

`tan 30° = "BD"/"AD"` 

`rArr 1/sqrt(3) = "R"/"H"`

`rArr 1/sqrt(3) = "R"/20`

`rArr "R" = 20/sqrt(3)  "cm"`

Now,

Volume of the wire = Volume of the frustum

`rArr pi(1/24)^2l = 1/3pih (R^2 + r^2 +"Rr")`

`= "l"/576 = 1/3xx10xx[(20/sqrt(3))^2 + (10/sqrt(3))^2 + (20/sqrt(3))(10/sqrt(3))]`

`rArr "l" = 576/3xx10xx[400/3+100/3+200/3]`

`= "l" = 576/3xx10xx700/3`

⇒ l = 448000 cm

∴ l = 4480 m

So, the length of the wire is 4480 m.