Advertisements
Advertisements
प्रश्न
A building is in the form of a cylinder surmounted by a hemispherical vaulted dome and contains `41 19/21 m^3` of air. If the internal diameter of dome is equal to its total height above the floor, find the height of the building?
उत्तर
Let total height of the building = Internal diameter of the dome = 2r m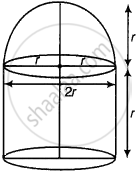
∴ Radius of building (or dome) = `(2r)/2` = r m
Height of cylinder = 2r – r = r m
∴ Volume of the cylinder = πr2(r) = πr3m3
And volume of hemispherical dome cylinder = `2/3 pir^3m^3`
∴ Total volume of the building
= Volume of the cylinder + Volume of hemispherical dome
= `(pir^3 + 2/3 pir^3)m^3`
= `5/3 pir^3m^3`
According to the question,
Volume of the building = Volume of the air
⇒ `5/3 pir^3 = 41 19/21`
⇒ `5/3 pir^3 = 880/21`
⇒ r3 = `(880 xx 7 xx 3)/(21 xx 22 xx 5)`
= `(40 xx 21)/(21 xx 5)`
= 8
⇒ r3 = 8
⇒ r = 2
∴ Height of the building = 2r
= 2 × 2
= 4 m
APPEARS IN
संबंधित प्रश्न
A vessel is in the form of an inverted cone. Its height is 8 cm and the radius of its top, which is open, is 5 cm. It is filled with water up to the brim. When lead shots, each of which is a sphere of radius 0.5 cm are dropped into the vessel, one-fourth of the water flows out. Find the number of lead shots dropped in the vessel.
A cylindrical vessel having diameter equal to its height is full of water which is poured into two identical cylindrical vessels with diameter 42cm and height 21cm which are filled completely. Find the diameter of cylindrical vessel?
Find the ratio of the volumes of a cylinder, a cone and a sphere, if each has the same diameter and same height?
A metallic solid right circular cone is of height 84 cm and the radius of its base is 21 cm. It is melted and recast into a solid sphere. Find the
diameter of the sphere.
A cubical ice-cream brick of edge 22 cm is to be distributed among some children by filling ice-cream cones of radius 2 cm and height 7 cm up to the brim. How many children will get the ice-cream cones?
The radii of two cylinders are in the ratio 2 : 3 and their heights are in the ratio 5 : 3. The ratio of their volumes is ______.
On increasing the radii of the base and the height of a cone by 20%, its volume will increase by
The radii of the base of a cylinder and a cone are in the ratio 3 : 4. If their heights are in the ratio 2 : 3, the ratio between their volumes is
A metal cube of side 11 cm is completely submerged in water contained in a cylindrical vessel with diameter 28 cm. Find the rise in the level of water.
From a solid cube of side 7 cm, a conical cavity of height 7 cm and radius 3 cm is hollowed out. Find the volume of the remaining solid.
