Advertisements
Advertisements
Question
A rocket is in the form of a right circular cylinder closed at the lower end and surmounted by a cone with the same radius as that of the cylinder. The diameter and height of the cylinder are 6 cm and 12 cm, respectively. If the slant height of the conical portion is 5 cm, find the total surface area and volume of the rocket [Use π = 3.14].
Solution
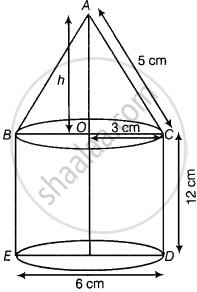
Since, rocket is the combination of a right circular cylinder and a cone.
Given, diameter of the cylinder = 6 cm
∴ Radius of the cylinder = `6/2` = 3 cm
And height of the cylinder = 12 cm
∴ Volume of the cylinder = πr2h
= 3.14 × (3)2 × 12
= 339.12 cm3
And curved surface area = 2πrh
= 2 × 3.14 × 3 × 12
= 226.08
Now, In right angled ΔAOC,
h = `sqrt(5^2 - 3^2)`
= `sqrt(25 - 9)`
= `sqrt(16)`
= 4
∴ Height of the cone, h = 4 cm
Radius of the cone, r = 3 cm
Now, volume of the cone
= `1/3 pir^2h`
= `1/3 xx 3.14 xx (3)^2 xx 4`
= `113.04/3`
= 37.68 cm3
And curved surface area = πrl
= 3.14 × 3 × 5
= 47.1
Hence, total volume of the rocket
= 339.12 + 37.68
= 376.8 cm3
And total surface area of the rocket
= CSA of cone + CSA of cylinder + Area of base of cylinder
= 47.1 + 226.08 + 28.26
= 301.44 cm2
APPEARS IN
RELATED QUESTIONS
How many silver coins, 1.75 cm in diameter and of thickness 2 mm, must be melted to form a cuboid of dimensions 5.5 cm × 10 cm × 3.5 cm? [Use π=22/7]
Water in canal, 6 m wide and 1.5 m deep, is flowing with a speed of 10 km/h. how much area will it irrigate in 30 minutes, if 8 cm of standing water is needed?
Three cubes of a metal whose edges are in the ratios 3 : 4 : 5 are melted and converted into a single cube whose diagonal is \[12\sqrt{3}\]. Find the edges of the three cubes.
16 glass spheres each of radius 2 cm are packed into a cuboidal box of internal dimensions \[16 cm \times 8 cm \times 8 cm\] and then the box is filled with water . Find the volume of the water filled in the box .
A tent is of the shape of a right circular cylinder upto a height of 3 metres and then becomes a right circular cone with a maximum height of 13.5 metres above the ground. Calculate the cost of painting the inner side of the tent at the rate of Rs 2 per square metre, if the radius of the base is 14 metres.
The diameters of the top and the bottom portions of a bucket are 42 cm and 28 cm respectively. If the height of the bucket is 24 cm, then the cost of painting its outer surface at the rate of 50 paise / cm2 is
If four times the sum of the areas of two circular faces of a cylinder of height 8 cm is equal to twice the curve surface area, then diameter of the cylinder is
If two solid-hemisphere s of same base radius r are joined together along their bases , then curved surface area of this new solid is
How many spherical lead shots of diameter 4 cm can be made out of a solid cube of lead whose edge measures 44 cm.
A solid metallic hemisphere of radius 8 cm is melted and recasted into a right circular cone of base radius 6 cm. Determine the height of the cone.
