Advertisements
Advertisements
Question
A hemisphere of lead of radius 6 cm is cast into a right circular cone of height 75 cm. Find the radius of the base of the cone.
Solution
We have,
Radius of the hemisphere, R = 6 cm and
Height of the cone, h = 75 cm
Let the radius of the base of the cone be r.
Now,
Volume of the cone =Volume of the hemisphere
`=> 1/3 pi"r"^2"h" = 2/3pi"R"^3`
`=> "r"^2 = (2"R"^3)/"h"`
`=> "r"^2 = 5.76 `
`=>"r"^2 = sqrt(5.76)`
∴ r =2.4 cm
So, the radius of the base of the cone is 2.4 cm.
APPEARS IN
RELATED QUESTIONS
Rain water, which falls on a flat rectangular surface of length 6cm and breath 4m is
transferred into a cylindrical vessel of internal radius 20cm. What will be the height of
water in the cylindrical vessel if a rainfall of 1cm has fallen____?
A vessel in the shape of cuboid ontains some water. If these identical spheres are immersed in the water, the level of water is increased by 2cm. if the area of base of cuboid is 160cm2 and its height 12cm, determine radius of any of spheres?
The diameters of internal and external surfaces of hollow spherical shell are 10cm and 6cm respectively. If it is melted and recast into a solid cylinder of length of 2`2/3`cm, find the
diameter of the cylinder.
A reservoir in the form of the frustum of a right circular cone contains 44 × 107 litres of water which fills it completely. The radii of the bottom and top of the reservoir are 50 metres and 100 metres respectively. Find the depth of water and the lateral surface area of the reservoir. (Take: π = 22/7)
A hollow cube of internal edge 22 cm is filled with spherical marbles of diameter 0.5 cm and `1/8` space of the cube remains unfilled. Number of marbles required is
The diameter of the base of a cone is 42 cm and its volume is 12936 cm3. Its height is
The sum of the inner and the outer curved surfaces of a hollow metallic cylinder is 1056 cm2 and the volume of material in it is 1056 cm3. Find its internal and external radii. Given that the height of the cylinder is 21 cm.
Water in a canal, 6 m wide and 1.5 m deep, is flowing with a speed of 10 km/hour. How much area will it irrigate in 30 mins; if 8 cm standing water is needed?
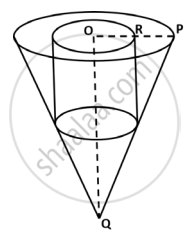
A solid piece of wooden cone is of radius OP = 7 cm and height OQ = 12 cm. A cylinder whose radius and height equal to half of that of the cone is drilled out from this piece of wooden cone. Find the volume of the remaining piece of wood. (Use, `pi = 22/7`)
A solid is in the shape of a hemisphere of radius 7 cm, surmounted by a cone of height 4 cm. The solid is immersed completely in a cylindrical container filled with water to a certain height. If the radius of the cylinder is 14 cm, find the rise in the water level.