Advertisements
Advertisements
Question
A vessel is in the form of an inverted cone. Its height is 8 cm and the radius of its top, which is open, is 5 cm. It is filled with water up to the brim. When lead shots, each of which is a sphere of radius 0.5 cm are dropped into the vessel, one-fourth of the water flows out. Find the number of lead shots dropped in the vessel.
Solution
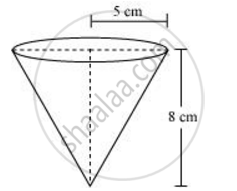
Height (h) of conical vessel = 8 cm
Radius (r1) of conical vessel = 5 cm
Radius (r2) of lead shots = 0.5 cm
Let n number of lead shots were dropped in the vessel.
Volume if water in concial vessel = `1/3 piR^2 h`
= `1/3 xx 22/7 xx (5) xx 8`
= `4400/21`cm3
Now, total volume of lead shots = `1/4` of [volume of water in the cone]
= `1/4 xx 4400/21`
= `1100/21` cm3
Since, radius of spherical lead shot (r)
= 0.5 cm = `5/10`cm3
∴ Volume of one lead shot = `4/3 pi r^3`
= `(4/3 xx 22/7 xx 5/10 xx 5/10 xx 5/10)` cm3
∴ Number of lead shots
= `"Total volume of lead shots"/"Volume of one lead shot"`
= `(1100/21)/((4 xx 22 xx 5 xx 5 xx 5)/(3 xx 7xx 1000))`
= 100
Thus, the required number of lead shorts = 100
APPEARS IN
RELATED QUESTIONS
A well of diameter 2m is dug14m deep. The earth taken out of it is spread evenly all around it to form an embankment of height 40cm. Find width of the embankment?
Find the volume of the largest right circular cone that can be cut out of a cube where edgeis 9cm?
Metal spheres each of radius 2cm are packed into a rectangular box of internal dimension 16cm x 8cm x 8cm when 16 spheres are packed the box is filled with preservative liquid. Find volume of this liquid?
A well with inner radius 4m is dug 14m deep earth taken out of it has been spread evenly all around a width of 3m it to form an embankment. Find the height of the embankment?
A circus tent has cylindrical shape surmounted by a conical roof. The radius of the cylindrical base is 20 m. The heights of the cylindrical and conical portions are 4.2 m and 2.1 m respectively. Find the volume of the tent.
A boiler is in the form of a cylinder 2 m long with hemispherical ends each of 2 metre diameter. Find the volume of the boiler.
A cylindrical vessel with internal diameter 10 cm and height 10.5 cm is full of water. A solid cone of base diameter 7 cm and height 6 cm is completely immersed in water. Find the value of water (i) displaced out of the cylinder (ii) left in the cylinder. (Take π 22/7)
12 spheres of the same size are made from melting a solid cylinder of 16 cm diameter and 2 cm height. The diameter of each sphere is
The adjoining figure represents a solid consisting of a cylinder surmounted by a cone at one end and a hemisphere at the other. Find the volume of the solid.
How many lead balls, each of radius 1 cm, can be made from a sphere of radius 8 cm?
Find the ratio of the volumes of a cylinder, a cone and a sphere, if each has the same diameter and same height?
A metallic solid right circular cone is of height 84 cm and the radius of its base is 21 cm. It is melted and recast into a solid sphere. Find the
diameter of the sphere.
Rainfall in an area is 5 cm. The volume of the water that falls on 2 hectares of land is
The diameter of the base of a cone is 42 cm and its volume is 12936 cm3. Its height is
The diameter of a sphere is 14 cm. Its volume is
A hemispherical bowl of internal diameter 30 cm is full of a liquid. This liquid is poured into cylindrical bottles of diameter 5 cm and height 6 cm each. How many bottles are required?
The radius of a solid right circular cylinder increases by 20% and its height decreases by 20%. Find the percentage change in its volume.
In the given figure, AB is the diameter of a circle with center O and OA = 7 cm. Find the area of the shaded region.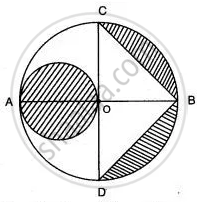
In a swimming pool measuring 90 m × 40 m, 150 men take a dip. If the average displacement of water by a man is 8 m3, then rise in water level is ______.
A hollow cube of internal edge 22 cm is filled with spherical marbles of diameter 0.5 cm and it is assumed that `1/8` space of the cube remains unfilled. Then the number of marbles that the cube can accomodate is ______.
