Advertisements
Advertisements
Question
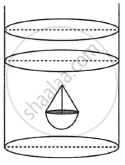
Find the ratio of the volumes of a cylinder, a cone and a sphere, if each has the same diameter and same height?
Solution
Let the radius of the sphere be r.
We have,
The radius of the cone = The radius of the cylinder = The radius of the sphere = r and
The height of the cylinder = The height of the cone = The height of the sphere = 2r
Now,
Volume of the cylinder `= pi"r"^2(2"r") = 2pi"r"^3`
Volume of the cone `= 1/3 pi"r"^2 (2"r") = 2/3 pi"r"^3` and
Volume of the sphere`=4/3pi"r"^3`
So,
The ratio of the Volumes of the cylinder, the cone and the sphere `= 2pi"r"^3 : 2/3pi"r"^3 : 4/3pi"r"^3`
`= 1 : 1/3 : 2/3`
`= 3 : 1 : 2`
So, the ratio of the volumes of the cylinder, the cone and the sphere is 3 : 1 : 2.
APPEARS IN
RELATED QUESTIONS
The height of a cone is 10 cm. The cone is divided into two parts using a plane parallel to its base at the middle of its height. Find the ratio of the volumes of the two parts.
A hemisphere tool of internal radius 9cm is full of liquid. This liquid is to be filled into
cylindrical shaped small bottles each of diameter 3cm and height 4cm. how many bottles are necessary to empty the bowl.
A solid metallic sphere of diameter 21 cm is melted and recast into small cones of diameter 3.5 cm and height 3 cm each. Find the number of cones so formed.
A metal cube of side 11 cm is completely submerged in water contained in a cylindrical vessel with diameter 28 cm. Find the rise in the level of water.
The volumes of two spheres are in the ratio 27 : 8. The ratio of their curved surface is ______.
The circumference of the edge of hemispherical bowl is 132 cm. When π is taken as `22/7`, the capacity of bowl in cm³ is ______.
An ice cream cone full of ice cream having radius 5 cm and height 10 cm as shown in the figure. Calculate the volume of ice cream, provided that its `1/6` part is left unfilled with ice cream.
A rectangular water tank of base 11 m × 6 m contains water upto a height of 5 m. If the water in the tank is transferred to a cylindrical tank of radius 3.5 m, find the height of the water level in the tank.
A building is in the form of a cylinder surmounted by a hemispherical vaulted dome and contains `41 19/21 m^3` of air. If the internal diameter of dome is equal to its total height above the floor, find the height of the building?
A solid is in the shape of a hemisphere of radius 7 cm, surmounted by a cone of height 4 cm. The solid is immersed completely in a cylindrical container filled with water to a certain height. If the radius of the cylinder is 14 cm, find the rise in the water level.