Advertisements
Advertisements
प्रश्न
Rachel, an engineering student, was asked to make a model shaped like a cylinder with two cones attached at its two ends by using a thin aluminium sheet. The diameter of the model is 3 cm and its length is 12 cm. if each cone has a height of 2 cm, find the volume of air contained in the model that Rachel made. (Assume the outer and inner dimensions of the model to be nearly the same.) [use `pi = 22/7`]
उत्तर
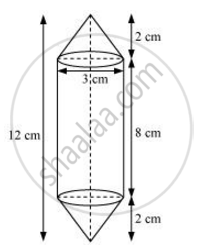
From the figure, it can be observed that
Height (h1) of each conical part = 2 cm
Height (h2) of cylindrical part = 12 − 2 × Height of conical part
= 12 − 2 × 2
= 8 cm
Radius (r) of cylindrical part = Radius of conical part = `3/2` cm
Volume of air present in the model = Volume of cylinder + 2 × Volume of cones
= `pir^2h_2 + 2xx1/3pir^2h_1`
= `22/7(3/2)^2(8)+2xx1/3pi(3/2)^2 (2)`
= `22/7xx9/4xx8+2/3pixx9/4xx2` cm3
= `22/7 xx 9/4 xx ((24 + 4)/3)` cm3
= `(22/7 xx 9/4 xx 28/3)` cm3
= 66 cm3
APPEARS IN
संबंधित प्रश्न
25 circular plates each of radius 10.5cm and thickness 1.6cm are placed one above the other to form a solid circular cylinder. Find the curved surface area and volume of cylinder so formed?
The surface area of a solid metallic sphere is 616 cm2. It is melted and recast into a cone of height 28 cm. Find the diameter of the base of the cone so formed (Use it =`22/7`)
A solid is in the shape of a cone surmounted on a hemisphere, the radius of each of them being 3.5 cm and the total height of the solid is 9.5 cm. Find the volume of the solid.
A solid is in the form of a right circular cone mounted on a hemisphere. The radius of the hemisphere is 2.1 cm and the height of the cone is 4 cm. The solid is placed in a cylindrical tub full of water in such a way that the whole solid is submerged in water. If the radius of the cylinder is 5 cm and its height is 9.8 cm, find the volume of the water left in the tub.
The diameter of a copper sphere is 18 cm. It is melted and drawn into a long wire of uniform cross-section. If the length of the wire is 108 m, find its diameter.
A hemisphere of lead of radius 6 cm is cast into a right circular cone of height 75 cm. Find the radius of the base of the cone.
A mason constructs a wall of dimensions (270 cm × 300 cm × 350 cm) with bricks, each of size (22.5 cm × 11.25 cm × 8.75 cm) and it is assumed that `1/8` space is covered by the mortar. Number of bricks used to construct the wall is ______.
A metallic cone of base radius 2.1 cm and height 8.4 cm is melted and moulded into a sphere. The radius of the sphere is
A solid metal cone with base radius 12 cm and height 24 cm is melted to form solid spherical balls of diameter 6 cm each. Find the number of balls formed.
A hemispherical bowl of internal diameter 30 cm is full of a liquid. This liquid is poured into cylindrical bottles of diameter 5 cm and height 6 cm each. How many bottles are required?
A solid metallic sphere of diameter 21 cm is melted and recast into small cones of diameter 3.5 cm and height 3 cm each. Find the number of cones so formed.
An iron pillar has some part in the form of a right circular cylinder and remaining in the form of a right circular cone. The radius of the base of each of cone and cylinder is 8 cm. The cylindrical part is 240 cm high and the conical part is 36 cm high. Find the weight of the pillar if one cubic cm of iron weight is 7.8 grams.
The radius of a wire is decreased to one third. If volume remains the same, the length will become ______.
Two solid cones A and B are placed in a cylinderical tube as shown in the figure. The ratio of their capacities are 2:1. Find the heights and capacities of cones. Also, find the volume of the remaining portion of the cylinder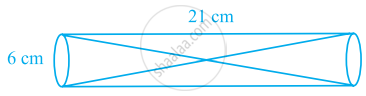
An ice cream cone full of ice cream having radius 5 cm and height 10 cm as shown in the figure. Calculate the volume of ice cream, provided that its `1/6` part is left unfilled with ice cream.
Find the number of metallic circular disc with 1.5 cm base diameter and of height 0.2 cm to be melted to form a right circular cylinder of height 10 cm and diameter 4.5 cm.
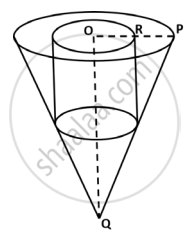
A solid piece of wooden cone is of radius OP = 7 cm and height OQ = 12 cm. A cylinder whose radius and height equal to half of that of the cone is drilled out from this piece of wooden cone. Find the volume of the remaining piece of wood. (Use, `pi = 22/7`)
A solid is in the shape of a right-circular cone surmounted on a hemisphere, the radius of each of them being 7 cm and the height of the cone is equal to its diameter. Find the volume of the solid.
A solid is in the shape of a hemisphere of radius 7 cm, surmounted by a cone of height 4 cm. The solid is immersed completely in a cylindrical container filled with water to a certain height. If the radius of the cylinder is 14 cm, find the rise in the water level.