Advertisements
Advertisements
प्रश्न
How many coins 1.75cm in diameter and 2mm thick must be melted to form a cuboid 11cm x 10cm x 75cm___?
उत्तर
Given that dimensions of a cuboid 11cm x 10cm x 75cm
So its volume (V1) = 11cm x 10cm x 7cm
= 11 x 10 x 7cm3 ..........(1)
Given diameter (d) = 1.75cm
Radius (r)`=d/2=1.75/2=0.875cm`
Thickness (h) =2mm = 0.2cm
Volume of acylinder =`pir^2h`
`V_2=pi(0.875)^2(0.2)cm^3` ........(2)
V1 = V2 x n
Since volume of a cuboid is equal to sum of n volume of ‘n’ coins
`n =V_1/V_2`
n = no of coins
`n=(11xx10xx7)/(n(0.875)^2(0.2))_`
n = 1600
∴No of coins (n) = 1600
APPEARS IN
संबंधित प्रश्न
A spherical glass vessel has a cylindrical neck 8 cm long, 2cm in diameter; the diameter of the spherical part is 8.5 cm. By measuring the amount of water it holds, a child finds its volume to be 345 cm3. Check whether she is correct, taking the above as the inside measurements, and π = 3.14
A heap of rice is in the form of a cone of base diameter 24 m and height 3.5 m. Find the volume of the rice. How much is canvas cloth required to just cover the heap?
25 circular plates each of radius 10.5cm and thickness 1.6cm are placed one above the other to form a solid circular cylinder. Find the curved surface area and volume of cylinder so formed?
A cylindrical tub of radius 5 cm and length 9.8 cm is full of water. A solid in the form of a right circular cone mounted on a hemisphere is immersed in the tub. If the radius of the hemisphere is immersed in the tub. If the radius of the hemi-sphere is 3.5 cm and height of the cone outside the hemisphere is 5 cm, find the volume of the water left in the tub (Take π = 22/7)
A hemispherical tank, of diameter 3 m, is full of water. It is being emptied by a pipe at the rate of \[3\frac{4}{7}\] litre per second. How much time will it take to make the tank half empty?\[\left[ Use \pi = \frac{22}{7} \right]\]
A hemispherical depression is cut out from one face of a cubical block of side 7 cm, such that the diameter of the hemisphere is equal to the edge of the cube. Find the surface area of the remaining solid. [Use π = \[\frac{22}{7}\]]
Choose the correct answer of the following question:
If the radius of the base of a right circular cylinder is halved, keeping the height the same, then the ratio of the volume of the cylinder thus obtained to the volume of original cylinder is
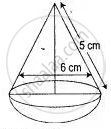
The given figure represents a hemisphere surmounted by a conical block of wood. The diameter of their bases is 6 cm each and the slant height of the cone is 5 cm. Calculate:
(i) the height of the cone.
(ii) the vol. of the solid.
A medicine-capsule is in the shape of a cylinder of diameter 0.5 cm with two hemispheres stuck to each of its ends. The length of entire capsule is 2 cm. The capacity of the capsule is ______.
Read the following passage and answer the questions given below.
|
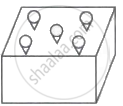
A solid cuboidal toy is made of wood. It has five cone-shaped cavities to hold toy carrots. The dimensions of the toy cuboid are – 10 cm × 10 cm × 8 cm. Each cone carved out – Radius = 2.1 cm and Height = 6 cm
|
- Find the volume of wood carved out to make five conical cavities.
- Find the volume of the wood in the final product.