Advertisements
Advertisements
प्रश्न
A pen stand made of wood is in the shape of a cuboid with four conical depressions and a cubical depression to hold the pens and pins, respectively. The dimension of the cuboid are 10 cm, 5 cm and 4 cm. The radius of each of the conical depressions is 0.5 cm and the depth is 2.1 cm. The edge of the cubical depression is 3 cm. Find the volume of the wood in the entire stand.
उत्तर
Given that, length of cuboid pen stand (l) = 10 cm
Breadth of cubiod pen stand (b) = 5 cm
And height of cuboid pen stand (h) = 4 cm

∴ Volume of cuboid pen stand
= l × b × h
= 10 × 5 × 4
= 200 cm3
Also, radius of conical depression (r) = 0.5 cm
And height (depth) of a conical depression (h1) = 2.1 cm
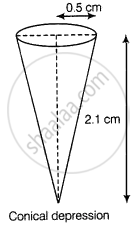
∴ Volume of a conical depression
= `1/3pir^2h_1`
= `1/3 xx 22/7 xx 0.5 xx 0.5 xx 2.1`
= `(22 xx 5 xx 5)/1000`
= `22/40`
= `11/20`
= 0.55 cm3
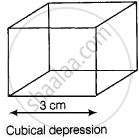
Also, given
Edge of cubical depression (a) = 3 cm
∴ Volume of cubical depression = (a)3 = (3) = 27 cm3
So, volume of 4 conical depressions
= 4 × Volume of a conical depression
= `4 xx 11/20`
= `11/5 cm^3`
Hence, the volume of wood in the entire pen stand
= Volume of cuboid pen stand – Volume of 4 conical depressions – Volume of a cubical depressions
= `200 - 11/5 - 27`
= `200 - 146/5`
= 200 – 29.2
= 170.8 cm3
So, the required volume of the wood in the entire stand is 170.8 cm3.
APPEARS IN
संबंधित प्रश्न
What length of a solid cylinder 2cm in diameter must be taken to recast into a hollow
cylinder of length 16cm, external diameter 20cm and thickness 2.5mm?
Find the volume of the largest right circular cone that can be cut out of a cube where edgeis 9cm?
A hemispherical tank, full of water, is emptied by a pipe at the rate of `25/7`litres per sec.
How much time will it take to empty half the tank if the diameter of the base of the tank is 3 m?
A solid piece of iron of dimensions 49 × 33 × 24 cm is moulded into a sphere. The radius of the sphere is
A metallic solid right circular cone is of height 84 cm and the radius of its base is 21 cm. It is melted and recast into a solid sphere. Find the
diameter of the sphere.
The radius of a solid right circular cylinder decreases by 20% and its height increases by 10%. Find the percentage change in its : volume
The given figure shows a solid formed of a solid cube of side 40 cm and a solid cylinder of radius 20 cm and height 50 cm attached to the cube as shown.
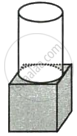
Find the volume and the total surface area of the whole solid. [Take π = 3.14].
In the given figure, AB is the diameter of a circle with center O and OA = 7 cm. Find the area of the shaded region.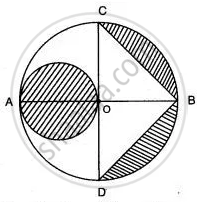
A solid piece of iron in the form of a cuboid of dimensions 49 cm × 33 cm × 24 cm, is moulded to form a solid sphere. The radius of the sphere is ______.
Marbles of diameter 1.4 cm are dropped into a cylindrical beaker of diameter 7 cm containing some water. Find the number of marbles that should be dropped into the beaker so that the water level rises by 5.6 cm.
