Advertisements
Advertisements
Question
A mason constructs a wall of dimensions 270 cm × 300 cm × 350 cm with the bricks each of size 22.5 cm × 11.25 cm × 8.75 cm and it is assumed that `1/8` space is covered by the mortar. Then the number of bricks used to construct the wall is ______.
Options
11100
11200
11000
11300
Solution
A mason constructs a wall of dimensions 270 cm × 300 cm × 350 cm with the bricks each of size 22.5 cm × 11.25 cm × 8.75 cm and it is assumed that `1/8` space is covered by the mortar. Then the number of bricks used to construct the wall is 11200.
Explanation:
Volume of the wall
= 270 × 300 × 350 ...[∵ Volume of cuboid = length × breadth × height]
= 28350000 cm3
Since, `1/8` space of wall is covered by mortar.
So, remaining space of wall
= Volume of wall – Volume of mortar
= `28350000 - 28350000 xx 1/8`
= 28350000 – 3543750
= 24806250 cm3
Now, volume of one brick
= 22.5 × 11.25 × 8.75 ...[∵ Volume of cuboid = length × breadth × height]
= 2214.844 cm3
∴ Required number of bricks = `24806250/2214.844` = 11200 (approx)
Hence, the number of bricks used to construct the wall is 11200.
APPEARS IN
RELATED QUESTIONS
How many spherical bullets each of 5cm in diameter can be cast from a rectangular block of metal 11 dm x 1m x 5 dm?
A conical flask is full of water. The flask has base radius r and height h. The water is poured into a cylindrical flask of base-radius mr. Find the height of water in the cylindrical flask.
A solid is in the shape of a cone surmounted on a hemisphere, the radius of each of them is being 3.5 cm and the total height of solid is 9.5 cm. Find the volume of the solid. (Use π = 22/7).
The radii of two cylinders are in the ratio of 2 : 3 and their heights are in the ratio of 5 : 3. Find the ratio of their volumes.
The ratio of the volumes of two spheres is 8 : 27. If r and R are the radii of spheres respectively, then (R – r) : r is ______.
The diameters of the two circular ends of the bucket are 44 cm and 24 cm. The height of the bucket is 35 cm. The capacity of the bucket is ______.
A cone of radius 8 cm and height 12 cm is divided into two parts by a plane through the mid-point of its axis parallel to its base. Find the ratio of the volumes of two parts.
From a solid cube of side 7 cm, a conical cavity of height 7 cm and radius 3 cm is hollowed out. Find the volume of the remaining solid.
Two solid cones A and B are placed in a cylinderical tube as shown in the figure. The ratio of their capacities are 2:1. Find the heights and capacities of cones. Also, find the volume of the remaining portion of the cylinder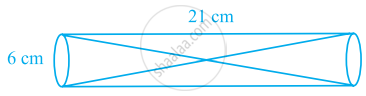
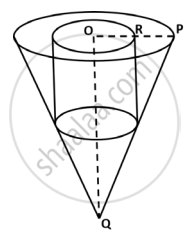
A solid piece of wooden cone is of radius OP = 7 cm and height OQ = 12 cm. A cylinder whose radius and height equal to half of that of the cone is drilled out from this piece of wooden cone. Find the volume of the remaining piece of wood. (Use, `pi = 22/7`)