Advertisements
Advertisements
प्रश्न
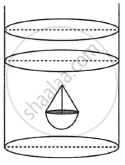
A cylindrical jar of radius 6cm contains oil. Iron sphere each of radius 1.5cm are immersed in the oil. How many spheres are necessary to raise level of the oil by two centimetress?
उत्तर
Given that radius of a cylindrical jar(r) = 6cm
Depth/height of cylindrical jar (h) = 2cm
Let no of balls be ‘n’
Volume of a cylinder = πr2h
V1`=22/7xx(6)^2xx2cm^3` ..........(1)
Radius of sphere 1.5cm
So volume of sphere`=4/3pir^3`
`V^2 = 4/3xx22/7(1.5)^3cm^3` .........(2)
Volume of cylindrical jar is equal to sum of volume of n spheres
Equating (1) and (2)
`22/7xx(6)^2xx2=nxx4/3xx22/4(1.5)^3`
`n=(v_1)/(v_2)`⇒ `n=(22/7xx(6)^2xx2)/(4/3xx22/7(1.5)^3`
n = 16
∴ No of spherical balls (n) = 16
APPEARS IN
संबंधित प्रश्न
50 circular plates each of diameter 14cm and thickness 0.5cm are placed one above other to form a right circular cylinder. Find its total surface area?
The largest sphere is to be curved out of a right circular of radius 7cm and height 14cm. find volume of sphere?
A toy is in the shape of a cone mounted on a hemisphere of same base radius. If the volume of the toy is 231 cm3 and its diameter is 7 cm, then find the height of the toy.
A metallic solid right circular cone is of height 84 cm and the radius of its base is 21 cm. It is melted and recast into a solid sphere. Find the
diameter of the sphere.
Choose the correct answer of the following question:
If the radius of the base of a right circular cylinder is halved, keeping the height the same, then the ratio of the volume of the cylinder thus obtained to the volume of original cylinder is
A hemispherical bowl of internal radius 9 cm is full of water. This water is to be filled in cylindrical bottles of diameter 3 cm and height 4 cm. Find the number of bottles needed in which the water can be filled.
Find the minimum length in cm and correct to nearest whole number of the thin metal sheet required to make a hollow and closed cylindrical box of diameter 20 cm and height 35 cm. Given that the width of the metal sheet is 1 m. Also, find the cost of the sheet at the rate of Rs. 56 per m.
Find the area of metal sheet required, if 10% of it is wasted in cutting, overlapping, etc.
An ice cream cone full of ice cream having radius 5 cm and height 10 cm as shown in the figure. Calculate the volume of ice cream, provided that its `1/6` part is left unfilled with ice cream.
Find the number of metallic circular disc with 1.5 cm base diameter and of height 0.2 cm to be melted to form a right circular cylinder of height 10 cm and diameter 4.5 cm.
A solid is in the shape of a hemisphere of radius 7 cm, surmounted by a cone of height 4 cm. The solid is immersed completely in a cylindrical container filled with water to a certain height. If the radius of the cylinder is 14 cm, find the rise in the water level.