Advertisements
Advertisements
प्रश्न
The ratio between the radius of the base and the height of a cylinder is 2 : 3. If the volume of the cylinder is 12936 cm3, then find the radius of the base of the cylinder.
उत्तर
Let the radius of the base and the height of the cylinder be r and h, respectively
We have,
r : h = 2 : 3 i.e `"r"/"h" = 2/3`
or `"h" = (3"r")/2` .........(i)
As,
Volume of the cylinder = 12936 cm3
`=> pi"r"^2"h" = 12936`
`=> 22/7xx"r"^2xx(3"r")/2 = 12936` [Using (i)]
`=> 33/7xx"r"^3=129336`
`=> "r"3 = 12936xx7/33`
⇒ r3 = 2744
`=> r = root(3)(2744)`
∴ r = 14 cm
o, the radius of the base of the cylinder is 14 cm.
APPEARS IN
संबंधित प्रश्न
A conical flask is full of water. The flask has base radius r and height h. The water is poured into a cylindrical flask of base-radius mr. Find the height of water in the cylindrical flask.
A cylindrical tub of radius 5 cm and length 9.8 cm is full of water. A solid in the form of a right circular cone mounted on a hemisphere is immersed in the tub. If the radius of the hemisphere is immersed in the tub. If the radius of the hemi-sphere is 3.5 cm and height of the cone outside the hemisphere is 5 cm, find the volume of the water left in the tub (Take π = 22/7)
A metallic solid right circular cone is of height 84 cm and the radius of its base is 21 cm. It is melted and recast into a solid sphere. Find the
diameter of the sphere.
Choose the correct answer of the following question:
If the radius of the base of a right circular cylinder is halved, keeping the height the same, then the ratio of the volume of the cylinder thus obtained to the volume of original cylinder is
Rainfall in an area is 5 cm. The volume of the water that falls on 2 hectares of land is
A piece of paper is in the shape of a semi-circular region of radius 10 cm. It is rolled to form a right circular cone. The slant height is ______.
A mason constructs a wall of dimensions 270 cm × 300 cm × 350 cm with the bricks each of size 22.5 cm × 11.25 cm × 8.75 cm and it is assumed that `1/8` space is covered by the mortar. Then the number of bricks used to construct the wall is ______.
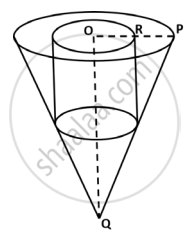
A solid piece of wooden cone is of radius OP = 7 cm and height OQ = 12 cm. A cylinder whose radius and height equal to half of that of the cone is drilled out from this piece of wooden cone. Find the volume of the remaining piece of wood. (Use, `pi = 22/7`)
A solid is in the shape of a right-circular cone surmounted on a hemisphere, the radius of each of them being 7 cm and the height of the cone is equal to its diameter. Find the volume of the solid.
A student was asked to make a model shaped like a cylinder with two cones attached to its ends by using a thin aluminium sheet. The diameter of the model is 3 cm and its total length is 12 cm. If each cone has a height of 2 cm, find the volume of air contained in the model.
