Advertisements
Advertisements
Question
A solid is in the shape of a cone standing on a hemisphere with both their radii being equal to 1 cm and the height of the cone is equal to its radius. Find the volume of the solid in terms of π.
Solution
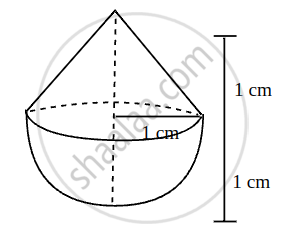
We have,
Height (h) of cone = Radius (r) of cone = 1 cm
Radius (r) of hemispherical = Radius of cone (r) = 1 cm
Volume of solid = Volume of cone + Volume of hemispherical
= `1/3 pir^2h + 2/3pir^3`
= `1/3pi[(1)^2 xx 1 + 2 xx (1)^3]`
= `1/3 pixx 1 xx 3`cm3
= π cm3
RELATED QUESTIONS
A heap of rice is in the form of a cone of base diameter 24 m and height 3.5 m. Find the volume of the rice. How much is canvas cloth required to just cover the heap?
Metal spheres each of radius 2cm are packed into a rectangular box of internal dimension 16cm x 8cm x 8cm when 16 spheres are packed the box is filled with preservative liquid. Find volume of this liquid?
A metallic right circular cone 20cm high and whose vertical angle is 90° is cut into two parts at the middle point of its axis by a plane parallel to base. If frustum so obtained bee
drawn into a wire of diameter
(1/16) cm find length of the wire?
A solid is in the shape of a cone standing on a hemisphere with both their radii being equal to 7 cm and the height of the cone is equal to its diameter. Find the volume of the solid. [Use`pi22/7`]
A toy is in the shape of a cone mounted on a hemisphere of same base radius. If the volume of the toy is 231 cm3 and its diameter is 7 cm, then find the height of the toy.
A metallic cylinder has radius 3 cm and height 5 cm. To reduce its weight, a conical hole is drilled in the cylinder. The conical hole has a radius of `3/2` cm and its depth is `8/9` cm. Calculate the ratio of the volume of metal left in the cylinder to the volume of metal taken out in conical shape.
A spherical shell of lead, whose external and internal diameters are 24 cm and 18 cm, is melted and recast into a right circular cylinder 37 cm high. Find the diameter of the base of the cylinder.
Twelve solid spheres of the same size are made by melting a solid metallic cylinder of base diameter 2 cm and height 16 cm. The diameter of each sphere is ______.
Rainfall in an area is 5 cm. The volume of the water that falls on 2 hectares of land is
The volumes of two cubes are in the ratio 1 : 27. The ratio of their surface area is
A hemispherical bowl of internal diameter 30 cm is full of a liquid. This liquid is poured into cylindrical bottles of diameter 5 cm and height 6 cm each. How many bottles are required?
The given figure shows a solid formed of a solid cube of side 40 cm and a solid cylinder of radius 20 cm and height 50 cm attached to the cube as shown.
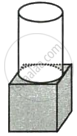
Find the volume and the total surface area of the whole solid. [Take π = 3.14].
The boundary of the shaded region in the given diagram consists of three semicircular areas, the smaller ones being equal and it’s diameter 5 cm, if the diameter of the larger one is 10 cm,
calculate:
(i) The length of the boundary,
(ii) The area of the shaded region. (Take π = 3.14)

The figure shows a running track surrounding a grassed enclosure PQRSTU. The enclosure consists of a rectangle PQST with a semicircular region at each end, PQ = 200 m; PT = 70 meters.
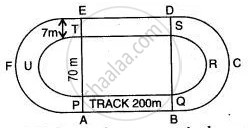
(i) Calculate the area of the grassed enclosure in m2.
(ii) Given that the track is of constant width 7 m, calculate the outer perimeter ABCDEF of the track. (Take π = `22/7`)
An iron pillar has some part in the form of a right circular cylinder and remaining in the form of a right circular cone. The radius of the base of each of cone and cylinder is 8 cm. The cylindrical part is 240 cm high and the conical part is 36 cm high. Find the weight of the pillar if one cubic cm of iron weight is 7.8 grams.
The radius of a wire is decreased to one third. If volume remains the same, the length will become ______.
A surahi is the combination of ______.
How many cubic centimetres of iron is required to construct an open box whose external dimensions are 36 cm, 25 cm and 16.5 cm provided the thickness of the iron is 1.5 cm. If one cubic cm of iron weighs 7.5 g, find the weight of the box.
Water flows through a cylindrical pipe, whose inner radius is 1 cm, at the rate of 80 cm/sec in an empty cylindrical tank, the radius of whose base is 40 cm. What is the rise of water level in tank in half an hour?
