Advertisements
Advertisements
प्रश्न
Two solid cones A and B are placed in a cylinderical tube as shown in the figure. The ratio of their capacities are 2:1. Find the heights and capacities of cones. Also, find the volume of the remaining portion of the cylinder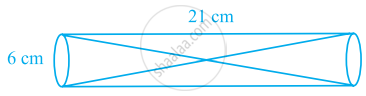
उत्तर
Let volume of cone A be 2V and volume of cone B be V.
Again, let height of the cone A = h1 cm,
Then height of cone B = (21 – h1) cm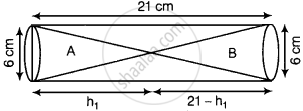
Given, diameter of the cone = 6 cm
∴ Radius of the cone = `6/2` = 3 cm
Now, volume of the cone,
A = 2V
= `1/3 pi"r"^2"h"`
= `1/3 pi(3)^2"h"_1`
⇒ V = `1/6 pi9"h"_1`
= `3/2 "h"_1pi` ...(i)
And volume of the cone,
B = V
= `1/3 pi(3)^2(21 - "h"_1)`
= 3π(21 – h1) ...(ii)
From equations (i) and (ii),
`3/2 "h"_1 pi` = 3π(21 – h1)
⇒ h1 = 2(21 – h1)
⇒ 3h1 = 42
⇒ h1 = `42/3` = 14 cm
∴ Height of cone,
B = 21 – h1
= 21 – 14
= 7 cm
Now, volume of the cone,
A = `3 xx 14 xx 22/7` = 132 cm2 ...[Using equation (i)]
And volume of the cone,
B = `1/3 xx 22/7 xx 9 xx 7` = 66 cm3 ...[Using equation (ii)]
Now, volume of the cylinder
= πr2h
= `22/7 (3)^2 xx 21`
= 594 cm3
∴ Required volume of the remaining portion
= Volume of the cylinder – (Volume of cone A + Volume of cone B)
= 594 – (132 + 66)
= 396 cm3
APPEARS IN
संबंधित प्रश्न
The height of a cone is 10 cm. The cone is divided into two parts using a plane parallel to its base at the middle of its height. Find the ratio of the volumes of the two parts.
Rain water, which falls on a flat rectangular surface of length 6cm and breath 4m is
transferred into a cylindrical vessel of internal radius 20cm. What will be the height of
water in the cylindrical vessel if a rainfall of 1cm has fallen____?
The diameter of a metallic sphere is equal to 9cm. it is melted and drawn into a long wire of diameter 2mm having uniform cross-section. Find the length of the wire?
How many coins 1.75cm in diameter and 2mm thick must be melted to form a cuboid 11cm x 10cm x 75cm___?
A metallic cone of radius 12 cm and height 24 cm is melted and made into spheres of radius 2 cm each. How many spheres are formed?
A solid rectangular block of dimensions 4.4 m, 2.6 m and 1 m is cast into a hollow cylindrical pipe of internal radius 30 cm and thickness 5 cm. Find the length of the pipe.
An ice cream cone full of ice cream having radius 5 cm and height 10 cm as shown in the figure. Calculate the volume of ice cream, provided that its `1/6` part is left unfilled with ice cream.
A wall 24 m long, 0.4 m thick and 6 m high is constructed with the bricks each of dimensions 25 cm × 16 cm × 10 cm. If the mortar occupies `1/10` th of the volume of the wall, then find the number of bricks used in constructing the wall.
A rectangular water tank of base 11 m × 6 m contains water upto a height of 5 m. If the water in the tank is transferred to a cylindrical tank of radius 3.5 m, find the height of the water level in the tank.
How many cubic centimetres of iron is required to construct an open box whose external dimensions are 36 cm, 25 cm and 16.5 cm provided the thickness of the iron is 1.5 cm. If one cubic cm of iron weighs 7.5 g, find the weight of the box.
