Advertisements
Advertisements
प्रश्न
A metallic cylinder has radius 3 cm and height 5 cm. To reduce its weight, a conical hole is drilled in the cylinder. The conical hole has a radius of `3/2` cm and its depth is `8/9` cm. Calculate the ratio of the volume of metal left in the cylinder to the volume of metal taken out in conical shape.
उत्तर
We have,
the base radius of the cylinder, R=3 cm
the height of the cylinder, H= 5 cm,
the base radius of the conical hole, r = `3/2` and
the height of the conical hole, h= `8/9` cm
Now,
Volume of the cylinder, V = πR2H
= π × 32 × 5
= 45π cm3
Also,
Volume of the cone removed from the cylinder, V=πR2H
`= π/3 xx (3/2)^2xx(8/9)`
`=(2π)/3 "cm"^3`
So, the volume of metal left in the cylinder, V' = V - v
`=45pi - (2pi)/3`
`=(133pi)/3 "cm"^3`
`therefore "The required ratio" = (V')/v`
`=(133pi/3)/((2pi)/3)`
`=133/2`
=133:2
So, the ratio of the volume of metal left in the cylinder to the volume of metal taken out in conical shape is 133 : 2.
APPEARS IN
संबंधित प्रश्न
The radii of two cylinders are in the ratio of 2 : 3 and their heights are in the ratio of 5 : 3. Find the ratio of their volumes.
A metallic cone of radius 12 cm and height 24 cm is melted and made into spheres of radius 2 cm each. How many spheres are formed?
A hollow sphere of external and internal diameters 8 cm and 4 cm, respectively is melted into a solid cone of base diameter 8 cm. Find the height of the cone.
Twelve solid spheres of the same size are made by melting a solid metallic cylinder of base diameter 2 cm and height 16 cm. The diameter of each sphere is ______.
A metallic cylinder of radius 8 cm and height 2 cm is melted and converted into a right circular cone of height 6 cm. The radius of the base of this cone is
In the given figure, AB is the diameter of a circle with center O and OA = 7 cm. Find the area of the shaded region.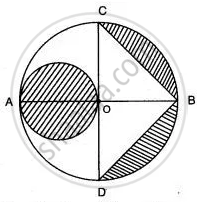
The radius of a wire is decreased to one third. If volume remains the same, the length will become ______.
A cone of radius 8 cm and height 12 cm is divided into two parts by a plane through the mid-point of its axis parallel to its base. Find the ratio of the volumes of two parts.
A solid iron cuboidal block of dimensions 4.4 m × 2.6 m × 1 m is recast into a hollow cylindrical pipe of internal radius 30 cm and thickness 5 cm. Find the length of the pipe.
From a soild cylinder of height 20 cm and diameter 12 cm, a conical cavity of height 8 cm and radius 6 cm is hallowed out. Find the total surface area of the remaining solid.
