Advertisements
Advertisements
प्रश्न
A wooden toy was made by scooping out a hemisphere of same radius from each end of a solid cylinder. If the height of the cylinder is 10 cm and its base is of radius 3.5 cm, then find the volume of wood in the toy.
उत्तर
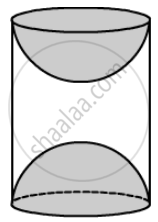
We have,
Radius of the cylinder = Radius of the hemispher = r = 3.5 cm and
Height of the cylinder, h = 10 cm
Now,
Volume of the toy = Volume of the cylinder - Volume of the two hemispheres
`= pi"r"^2"h"-2xx2/3pi"r"^3`
`=pi"r"^2("h" - (4"r")/3)`
`= 22/7xx3.5xx3.5xx(10-(4xx3.5)/(3))`
`=38.5xx(10-14/3)`
`=38.5xx16/3`
`=616/3 "cm"^3`
≈ 205.33 cm3
So, the volume of wood in the toy is `616/3` cm3 or 205.33 cm3
APPEARS IN
संबंधित प्रश्न
A cylindrical vessel having diameter equal to its height is full of water which is poured into two identical cylindrical vessels with diameter 42cm and height 21cm which are filled completely. Find the diameter of cylindrical vessel?
From a solid cylinder of height 14 cm and base diameter 7 cm, two equal conical holes each of radius 2.1 cm and height 4 cm are cut off. Find the volume of the remaining solid.
How many lead balls, each of radius 1 cm, can be made from a sphere of radius 8 cm?
A surahi is a combination of
A hemispherical bowl of internal radius 9 cm is full of water. This water is to be filled in cylindrical bottles of diameter 3 cm and height 4 cm. Find the number of bottles needed in which the water can be filled.
The radius of a solid right circular cylinder increases by 20% and its height decreases by 20%. Find the percentage change in its volume.
Find the minimum length in cm and correct to nearest whole number of the thin metal sheet required to make a hollow and closed cylindrical box of diameter 20 cm and height 35 cm. Given that the width of the metal sheet is 1 m. Also, find the cost of the sheet at the rate of Rs. 56 per m.
Find the area of metal sheet required, if 10% of it is wasted in cutting, overlapping, etc.
The radius of a wire is decreased to one third. If volume remains the same, the length will become ______.
The diameters of the two circular ends of the bucket are 44 cm and 24 cm. The height of the bucket is 35 cm. The capacity of the bucket is ______.
A rectangular water tank of base 11 m × 6 m contains water upto a height of 5 m. If the water in the tank is transferred to a cylindrical tank of radius 3.5 m, find the height of the water level in the tank.
