Advertisements
Advertisements
Question
How many balls each of radius 1cm can be made from a solid sphere of lead of radius
8cm?
Solution
Given that a solid sphere f radius (r1)= 8 cm
With this sphere we have to make spherical balls of radius (r2)=1cm
since we don’t know no of balls let us assume that no of balls formed be ‘n’
We know that
Volume of sphere=`4/3 pir^2`
Volume of solid sphere should be equal to sum of volumes of n spherical balls
`nxx4/3pi(1)^3=4/3pir^3`
`n=(4/3pi(8)^3)/(4/3pi(1)^3)`
n=`8^3`
n=512
∴hence 512 no of balls can be made of radius 1cm from a solid sphere of radius
8cm
APPEARS IN
RELATED QUESTIONS
If the volumes of two cones are in the ratio of 1:4 and their diameters are in the ratio of 4:5, then find the ratio of their heights.
A toy is in the shape of a cone mounted on a hemisphere of same base radius. If the volume of the toy is 231 cm3 and its diameter is 7 cm, then find the height of the toy.
The radii of two cylinders are in the ratio of 2 : 3 and their heights are in the ratio of 5 : 3. Find the ratio of their volumes.
A cylinder with base radius 8 cm and height 2 cm is melted to form a cone of height 6 cm. Calculate the radius of the base of the cone.
Twelve solid spheres of the same size are made by melting a solid metallic cylinder of base diameter 2 cm and height 16 cm. The diameter of each sphere is ______.
The radii of two cylinders are in the ratio 2 : 3 and their heights are in the ratio 5 : 3. The ratio of their volumes is ______.
How many shots each having diameter 3 cm can be made from a cuboidal lead solid of dimensions 9 cm × 11cm × 12cm?
Two solid cones A and B are placed in a cylinderical tube as shown in the figure. The ratio of their capacities are 2:1. Find the heights and capacities of cones. Also, find the volume of the remaining portion of the cylinder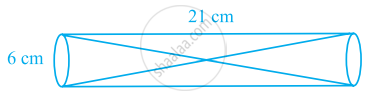
Find the number of metallic circular disc with 1.5 cm base diameter and of height 0.2 cm to be melted to form a right circular cylinder of height 10 cm and diameter 4.5 cm.
A heap of rice is in the form of a cone of diameter 9 m and height 3.5 m. Find the volume of the rice. How much canvas cloth is required to just cover the heap?
