Advertisements
Advertisements
Question
A(2, 5), B(1, 0), C(−4, 3) and D(–3, 8) are the vertices of quadrilateral ABCD. Find the co-ordinates of the mid-points of AC and BD. Give a special name to the quadrilateral.
Solution
Co-ordinates of A = (2, 5), of B = (1, 0), of C = (−4, 3) and of D = (−3, 8)
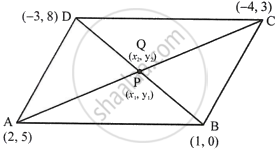
Let the mid-point of AC is P(x1, y1)
∴ Co-ordinates of mid-point of AC will be
`(x_1, y_1) = ((2 - 4)/2, (5 + 3)/2)`
=`((-2)/2, 8/2)`
= (−1, 4)
Let the mid-point of BD is Q(x2, y2)
Co-ordinates of mid-point of BD will be
∴ `(x_2, y_2) = ((1 + (-3))/2, (0 + 8)/2)`
= `((1 - 3)/2, 8/2)`
= `((-2)/2, 8/2)`
= (−1, 4)
∵ Co-ordinates of mid-points AC and BD are the same.
∴ The quadrilateral is a parallelogram.
APPEARS IN
RELATED QUESTIONS
Given M is the mid-point of AB, find the co-ordinates of B; if A = (3, –1) and M = (–1, 3).
Calculate the co-ordinates of the centroid of the triangle ABC, if A = (7, –2), B = (0, 1) and C =(–1, 4).
Prove that the points A(–5, 4); B(–1, –2) and C(5, 2) are the vertices of an isosceles right-angled triangle. Find the co-ordinates of D so that ABCD is a square.
Find the coordinates of point P if P divides the line segment joining the points A(–1, 7) and B(4, –3) in the ratio 2 : 3.
Point P is the centre of the circle and AB is a diameter . Find the coordinates of point B if coordinates of point A and P are (2, –3) and (–2, 0) respectively.
(4, 2) and (-1, 5) are the adjacent vertices ofa parallelogram. (-3, 2) are the coordinates of the points of intersection of its diagonals. Find the coordinates of the other two vertices.
Find the centroid of a triangle whose vertices are (3, -5), (-7, 4) and ( 10, -2).
ABC is a triangle whose vertices are A(-4, 2), B(O, 2) and C(-2, -4). D. E and Fare the midpoint of the sides BC, CA and AB respectively. Prove that the centroid of the Δ ABC coincides with the centroid of the Δ DEF.
Find coordinates of midpoint of the segment joining points (0, 2) and (12, 14)
If the vertices of a triangle are (1, 3), (2, - 4) and (-3, 1). Then the co-ordinate of its centroid is:
