Advertisements
Advertisements
Question
ABC is a triangle whose vertices are A(-4, 2), B(O, 2) and C(-2, -4). D. E and Fare the midpoint of the sides BC, CA and AB respectively. Prove that the centroid of the Δ ABC coincides with the centroid of the Δ DEF.
Solution
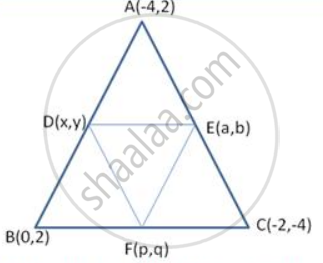
Let D , E and F be the midpoints of the sides AB , AC and BC of Δ ABC respectively.
∴ AD : DB = BF : FC = AE : EC = 1 : 1
Coordinates of D are ,
D (x , y) = D `((0 - 4)/2 , (2 + 2)/3) = "D" (-2 , 2)`
Similarly ,
E (a , b) = E `((-4 - 2)/2 , (2 - 4)/2)` = E (-3 , -1)
and ,
F (p,q) = F `((0 - 2)/2 , (2 - 4)/2)` = F (-1 , -1)
Coordinates of centroid of Δ ABC are ,
`= ((-4-2+0)/3 , (2 - 4 + 2)/3)` = (-2 , 0)
Coordinates of centroid of Δ DEF are ,
`= ((-2-3-1)/3 , (2 - 1 - 1)/3) = (-2 , 0)`
Thud the centroid of Δ DEF coincides with centroid of Δ DEF.
APPEARS IN
RELATED QUESTIONS
Points A(–5, x), B(y, 7) and C(1, –3) are collinear (i.e. lie on the same straight line) such that AB = BC. Calculate the values of x and y.
Find the coordinates of point P if P divides the line segment joining the points A(–1, 7) and B(4, –3) in the ratio 2 : 3.
In the following example find the co-ordinate of point A which divides segment PQ in the ratio a : b.
P(–3, 7), Q(1, –4), a : b = 2 : 1
Write the co-ordinates of the point of intersection of graphs of
equations x = 2 and y = -3.
Complete the table below the graph with the help of the following graph.

| Sr. No. | First point | Second point | Co-ordinates of first point (x1 , y1) | Co-ordinates of second point (x2 , y2) | `(y_2 - y_2)/(x_2 - x_2)` |
| 1 | C | E | (1, 0) | (3,4) | `4/2=2` |
| 2 | A | B | (-1,-4) | (0,-2) | `2/1 = 2` |
| 3 | B | D | (0,-2) | (2,2) | `4/2=2` |
Find the midpoint of the line segment joining the following pair of point :
(3a-2b, Sa+7b) and (a+4b, a-3b)
The coordinates of the end points of the diameter of a circle are (3, 1) and (7, 11). Find the coordinates of the centre of the circle.
The points A(−5, 4), B(−1, −2) and C(5, 2) are the vertices of an isosceles right-angled triangle where the right angle is at B. Find the coordinates of D so that ABCD is a square
A(−3, 2), B(3, 2) and C(−3, −2) are the vertices of the right triangle, right angled at A. Show that the mid-point of the hypotenuse is equidistant from the vertices
If A(5, 4), B(–3, –2) and C(1, –8) are the vertices of a ∆ABC. Segment AD is median. Find the length of seg AD:
