Advertisements
Advertisements
Question
In the following example find the co-ordinate of point A which divides segment PQ in the ratio a : b.
P(–3, 7), Q(1, –4), a : b = 2 : 1
Solution
Let the coordinates of point A be (x, y).
P(–3, 7), Q(1, –4), a : b = 2 : 1
Using section formula
\[x = \frac{2 \times 1 + 1 \times \left( - 3 \right)}{2 + 1} = \frac{2 - 3}{3} = \frac{- 1}{3}\]
\[y = \frac{2 \times \left( - 4 \right) + 1 \times 7}{2 + 1} = \frac{- 8 + 7}{3} = \frac{- 1}{3}\]
\[\left( x, y \right) = \left( \frac{- 1}{3}, \frac{- 1}{3} \right)\]
APPEARS IN
RELATED QUESTIONS
P(4, 2) and Q(–1, 5) are the vertices of parallelogram PQRS and (–3, 2) are the co-ordinates of the point of intersection of its diagonals. Find co-ordinates of R and S.
Points P(a, −4), Q(−2, b) and R(0, 2) are collinear. If Q lies between P and R, such that PR = 2QR, calculate the values of a and b.
Calculate the co-ordinates of the centroid of the triangle ABC, if A = (7, –2), B = (0, 1) and C =(–1, 4).
In the following example find the co-ordinate of point A which divides segment PQ in the ratio a : b.
P(–2, –5), Q(4, 3), a : b = 3 : 4
Find the coordinates of midpoint of the segment joining the points (22, 20) and (0, 16).
Point P is the midpoint of seg AB. If co-ordinates of A and B are (-4, 2) and (6, 2) respectively then find the co-ordinates of point P.
(A) (-1,2) (B) (1,2) (C) (1,-2) (D) (-1,-2)
Complete the table below the graph with the help of the following graph.

| Sr. No. | First point | Second point | Co-ordinates of first point (x1 , y1) | Co-ordinates of second point (x2 , y2) | `(y_2 - y_2)/(x_2 - x_2)` |
| 1 | C | E | (1, 0) | (3,4) | `4/2=2` |
| 2 | A | B | (-1,-4) | (0,-2) | `2/1 = 2` |
| 3 | B | D | (0,-2) | (2,2) | `4/2=2` |
Find the centroid of a triangle whose vertices are (3, -5), (-7, 4) and ( 10, -2).
Two vertices of a triangle are (1, 4) and (3, 1). If the centroid of the triangle is the origin, find the third vertex.
AB is a diameter of a circle with centre 0. If the ooordinates of A and 0 are ( 1, 4) and (3, 6 ). Find the ooordinates of B and the length of the diameter.
A(3, 1), B(y, 4) and C(1, x) are vertices of a triangle ABC and G(3, 4) is its centroid. Find the values of x and y. Also, find the length of side BC.
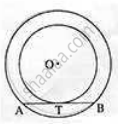
As shown in the figure. two concentric circles are given and line AB is the tangent to the smaller circle at T. Shown that T is the midpoint of Seg AB
The midpoint of the line segment joining (2a, 4) and (-2, 2b) is (1, 2a+1). Find the value of a and b.
show that the points A(- 1, 2), B(2, 5) and C(- 5, – 2) are collinear.
Find the mid-point of the line segment joining the points
(8, −2) and (−8, 0)
Find the mid-point of the line segment joining the points
(a, b) and (a + 2b, 2a – b)
O(0, 0) is the centre of a circle whose one chord is AB, where the points A and B are (8, 6) and (10, 0) respectively. OD is the perpendicular from the centre to the chord AB. Find the coordinates of the mid-point of OD.
The points A(−3, 6), B(0, 7) and C(1, 9) are the mid-points of the sides DE, EF and FD of a triangle DEF. Show that the quadrilateral ABCD is a parallelogram.
A(−3, 2), B(3, 2) and C(−3, −2) are the vertices of the right triangle, right angled at A. Show that the mid-point of the hypotenuse is equidistant from the vertices
The ratio in which the x-axis divides the line segment joining the points A (a1, b1) and B (a2, b2) is
