Advertisements
Advertisements
Question
As shown in the figure. two concentric circles are given and line AB is the tangent to the smaller circle at T. Shown that T is the midpoint of Seg AB
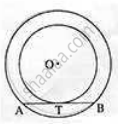
Solution
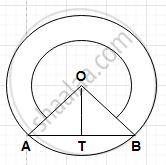
proof OT is perpendicular to AB (as AB = tangent)
other Method -
In ΔAOT, ΔOTB
∠OTB = ∠OTB = 90°
OT = OT = common
OA = OB = radii
∴ ΔAOT ≅ ΔBOT
∴ At = BT ( by cpct)
Now, we know that if a perpendicular is drawn to any chord from the centre, it bisects the chord.
∴ AT = TB
Hence, This midpoint of AB.
APPEARS IN
RELATED QUESTIONS
Find the mid-point of the line segment joining the points:
(–6, 7) and (3, 5)
Given a line ABCD in which AB = BC = CD, B = (0, 3) and C = (1, 8). Find the co-ordinates of A and D.
A(2, 5), B(1, 0), C(−4, 3) and D(–3, 8) are the vertices of quadrilateral ABCD. Find the co-ordinates of the mid-points of AC and BD. Give a special name to the quadrilateral.
Calculate the co-ordinates of the centroid of the triangle ABC, if A = (7, –2), B = (0, 1) and C =(–1, 4).
The co-ordinates of the centroid of a triangle PQR are (2, –5). If Q = (–6, 5) and R = (11, 8); calculate the co-ordinates of vertex P.
M is the mid-point of the line segment joining the points A(–3, 7) and B(9, –1). Find the coordinates of point M. Further, if R(2, 2) divides the line segment joining M and the origin in the ratio p : q, find the ratio p : q.
Find the coordinates of midpoint of the segment joining the points (22, 20) and (0, 16).
Complete the table below the graph with the help of the following graph.

| Sr. No. | First point | Second point | Co-ordinates of first point (x1 , y1) | Co-ordinates of second point (x2 , y2) | `(y_2 - y_2)/(x_2 - x_2)` |
| 1 | C | E | (1, 0) | (3,4) | `4/2=2` |
| 2 | A | B | (-1,-4) | (0,-2) | `2/1 = 2` |
| 3 | B | D | (0,-2) | (2,2) | `4/2=2` |
Find the midpoint of the line segment joining the following pair of point :
( a+3, 5b), (3a-1, 3b +4).
The coordinates of the centroid I of triangle PQR are (2, 5). If Q = (-6, 5) and R = (7, 8). Calculate the coordinates of vertex P.
The midpoints of three sides of a triangle are (1, 2), (2, -3) and (3, 4). Find the centroid of the triangle.
Let A(-a, 0), B(0, a) and C(α , β) be the vertices of the L1 ABC and G be its centroid . Prove that
GA2 + GB2 + GC2 = `1/3` (AB2 + BC2 + CA2)
The mid point of the line segment joining the points (p, 2) and (3, 6) is (2, q). Find the numerical values of a and b.
Point M is the mid-point of segment AB. If AB = 8.6 cm, then find AM.
Find the mid-point of the line segment joining the points
(8, −2) and (−8, 0)
The centre of a circle is (−4, 2). If one end of the diameter of the circle is (−3, 7) then find the other end
If the coordinates of one end of a diameter of a circle is (3, 4) and the coordinates of its centre is (−3, 2), then the coordinate of the other end of the diameter is
The coordinates of diameter AB of a circle are A(2, 7) and B(4, 5), then find the coordinates of the centre
Find the coordinates of midpoint of segment joining (22, 20) and (0, 16)
Find the coordinates of point P where P is the midpoint of a line segment AB with A(–4, 2) and B(6, 2).
Solution :

Suppose, (–4, 2) = (x1, y1) and (6, 2) = (x2, y2) and co-ordinates of P are (x, y).
∴ According to the midpoint theorem,
x = `(x_1 + x_2)/2 = (square + 6)/2 = square/2 = square`
y = `(y_1 + y_2)/2 = (2 + square)/2 = 4/2 = square`
∴ Co-ordinates of midpoint P are `square`.
