Advertisements
Advertisements
Question
The mid point of the line segment joining the points (p, 2) and (3, 6) is (2, q). Find the numerical values of a and b.
Solution

AC : CB = 1 : 1
Coordinates of C are ,
C (2 , q) = C `(("p" + 3)/2 , (2 + 6)/2)`
`2 = ("p" + 3)/2` , q = 4
4 = p + 3 , q = 4
p = 1 , q = 4
the values of p and q are 1 and 4 respectively.
APPEARS IN
RELATED QUESTIONS
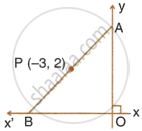
P(–3, 2) is the mid-point of line segment AB as shown in the given figure. Find the co-ordinates of points A and B.
In the following example find the co-ordinate of point A which divides segment PQ in the ratio a : b.
P(–3, 7), Q(1, –4), a : b = 2 : 1
In the following example find the co-ordinate of point A which divides segment PQ in the ratio a : b.
P(2, 6), Q(–4, 1), a : b = 1 : 2
A(6, -2), B(3, -2) and C(S, 6) are the three vertices of a parallelogram ABCD. Find the coordinates of the fourth vertex c.
The midpoints of three sides of a triangle are (1, 2), (2, -3) and (3, 4). Find the centroid of the triangle.
A lies on the x - axis amd B lies on the y -axis . The midpoint of the line segment AB is (4 , -3). Find the coordinates of A and B .
The midpoint of the line segment joining (2a, 4) and (-2, 2b) is (1, 2a+1). Find the value of a and b.
show that the points A(- 1, 2), B(2, 5) and C(- 5, – 2) are collinear.
In what ratio does the y-axis divides the line joining the points (−5, 1) and (2, 3) internally
Find coordinates of the midpoint of a segment joining point A(–1, 1) and point B(5, –7)
Solution: Suppose A(x1, y1) and B(x2, y2)
x1 = –1, y1 = 1 and x2 = 5, y2 = –7
Using midpoint formula,
∴ Coordinates of midpoint of segment AB
= `((x_1 + x_2)/2, (y_1+ y_2)/2)`
= `(square/2, square/2)`
∴ Coordinates of the midpoint = `(4/2, square/2)`
∴ Coordinates of the midpoint = `(2, square)`
If A(5, 4), B(–3, –2) and C(1, –8) are the vertices of a ∆ABC. Segment AD is median. Find the length of seg AD:
