Advertisements
Advertisements
Question
In the following example find the co-ordinate of point A which divides segment PQ in the ratio a : b.
P(–2, –5), Q(4, 3), a : b = 3 : 4
Solution
Let the coordinates of point A be (x, y).
P(–2, –5), Q(4, 3), a : b = 3 : 4
Using section formula
\[x = \frac{3 \times 4 + 4 \times \left( - 2 \right)}{3 + 4} = \frac{12 - 8}{7} = \frac{4}{7}\]
\[y = \frac{3 \times 3 + 4 \times \left( - 5 \right)}{3 + 4} = \frac{9 - 20}{7} = \frac{- 11}{7}\]
\[\left( x, y \right) = \left( \frac{4}{7}, \frac{- 11}{7} \right)\]
APPEARS IN
RELATED QUESTIONS
A(5, 3), B(–1, 1) and C(7, –3) are the vertices of triangle ABC. If L is the mid-point of AB and M is the mid-point of AC, show that : `LM = 1/2 BC`.
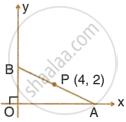
In the given figure, P(4, 2) is mid-point of line segment AB. Find the co-ordinates of A and B.
A(2, 5), B(1, 0), C(−4, 3) and D(–3, 8) are the vertices of quadrilateral ABCD. Find the co-ordinates of the mid-points of AC and BD. Give a special name to the quadrilateral.
Points P(a, −4), Q(−2, b) and R(0, 2) are collinear. If Q lies between P and R, such that PR = 2QR, calculate the values of a and b.
Write the co-ordinates of the point of intersection of graphs of
equations x = 2 and y = -3.
Complete the table below the graph with the help of the following graph.

| Sr. No. | First point | Second point | Co-ordinates of first point (x1 , y1) | Co-ordinates of second point (x2 , y2) | `(y_2 - y_2)/(x_2 - x_2)` |
| 1 | C | E | (1, 0) | (3,4) | `4/2=2` |
| 2 | A | B | (-1,-4) | (0,-2) | `2/1 = 2` |
| 3 | B | D | (0,-2) | (2,2) | `4/2=2` |
A(6, -2), B(3, -2) and C(S, 6) are the three vertices of a parallelogram ABCD. Find the coordinates of the fourth vertex c.
(4, 2) and (-1, 5) are the adjacent vertices ofa parallelogram. (-3, 2) are the coordinates of the points of intersection of its diagonals. Find the coordinates of the other two vertices.
Three consecutive vertices of a parallelogram ABCD are A(S, 5), B(-7, -5) and C(-5, 5). Find the coordinates of the fourth vertex D.
A lies on the x - axis amd B lies on the y -axis . The midpoint of the line segment AB is (4 , -3). Find the coordinates of A and B .
P , Q and R are collinear points such that PQ = QR . IF the coordinates of P , Q and R are (-5 , x) , (y , 7) , (1 , -3) respectively, find the values of x and y.
If P(–b, 9a – 2) divides the line segment joining the points A(–3, 3a + 1) and B(5, 8a) in the ratio 3: 1, find the values of a and b.
Point M is the mid-point of segment AB. If AB = 8.6 cm, then find AM.
O(0, 0) is the centre of a circle whose one chord is AB, where the points A and B are (8, 6) and (10, 0) respectively. OD is the perpendicular from the centre to the chord AB. Find the coordinates of the mid-point of OD.
Point P is midpoint of segment AB where A(– 4, 2) and B(6, 2), then the coordinates of P are ______
Find the coordinates of midpoint of segment joining (22, 20) and (0, 16)
If the vertices of a triangle are (1, 3), (2, - 4) and (-3, 1). Then the co-ordinate of its centroid is:
