Advertisements
Advertisements
Question
If P(–b, 9a – 2) divides the line segment joining the points A(–3, 3a + 1) and B(5, 8a) in the ratio 3: 1, find the values of a and b.
Solution
Take (x1, y1) = (–3, 3a + 1); (x2, y2) = B(5, 8a)
And (x, y) = (–b, 9a – 2)
Here m1 = 3 and m2 =1
Coordinate of P(x, y) = `((m_1x_2 + m_2x_1)/(m_1 _ m_2), (m_1y_2 + m_2y_1)/(m_1 + m_2))`
`=> x = (m_1x_2 + m_2x_1)/(m_1 _ m_2)` and `y = (m_1y_2 + m_2y_1)/(m_1 + m_2)`
`=> -b = (3 xx 5 + 1 xx (-3))/(3 + 1)` and `9a - 2 = (3xx8a + 1(3a + 1))/(3 + 1)`
`=> -b = (15 - 3)/4` and `9a - 2 = (24a + 3a + 1)/4`
`=>` –4b = 12 and 36a – 8 = 27a + 1
`=>` b = –3 and 9a = 9
a = 1 and b = –3
APPEARS IN
RELATED QUESTIONS
Given M is the mid-point of AB, find the co-ordinates of A; if M = (1, 7) and B = (–5, 10).
P(4, 2) and Q(–1, 5) are the vertices of parallelogram PQRS and (–3, 2) are the co-ordinates of the point of intersection of its diagonals. Find co-ordinates of R and S.
Find the coordinates of midpoint of the segment joining the points (22, 20) and (0, 16).
Write the co-ordinates of the point of intersection of graphs of
equations x = 2 and y = -3.
(4, 2) and (-1, 5) are the adjacent vertices ofa parallelogram. (-3, 2) are the coordinates of the points of intersection of its diagonals. Find the coordinates of the other two vertices.
Let A(-a, 0), B(0, a) and C(α , β) be the vertices of the L1 ABC and G be its centroid . Prove that
GA2 + GB2 + GC2 = `1/3` (AB2 + BC2 + CA2)
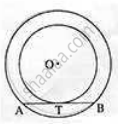
As shown in the figure. two concentric circles are given and line AB is the tangent to the smaller circle at T. Shown that T is the midpoint of Seg AB
The coordinates of diameter AB of a circle are A(2, 7) and B(4, 5), then find the coordinates of the centre
Find the coordinates of midpoint of segment joining (22, 20) and (0, 16)
Find the co-ordinates of centroid of a triangle if points D(–7, 6), E(8, 5) and F(2, –2) are the mid-points of the sides of that triangle.
